
分析 (1)分别求出sinθ和cosθ的值,从而求出B点的坐标;
(2)根据三角函数的公式代入求出即可.
解答 解:(1)点A是单位圆与x轴正半轴的交点,点B在第二象限
设B(x,y),则y=sinθ=$\frac{4}{5}$,
x=cosθ=-$\sqrt{1{-sin}^{2}θ}$=-$\frac{3}{5}$,
∴B点的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$);
(2)$\frac{sin(π+θ)+2sin(\frac{π}{2}+θ)}{2cos(π-θ)}$
=$\frac{-sinθ+2cosθ}{-2cosθ}$
=$\frac{-\frac{4}{5}-\frac{6}{5}}{\frac{6}{5}}$
=-$\frac{5}{3}$.
点评 本题考查了三角函数的定义及其基本关系,熟练掌握三角函数的公式是解题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
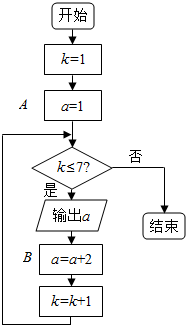 按图所示的程序框图操作:
按图所示的程序框图操作:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{3}$ | B. | -$\frac{2\sqrt{3}}{3}$ | C. | 0 | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.8-0.1>0.8-0.2 | B. | log0.53>log0.52 | C. | sin$\frac{2π}{5}$<sin$\frac{π}{5}$ | D. | 0.7-0.3>0.82.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lnx2,g(x)=2lnx | B. | f(x)=x,g(x)=($\sqrt{x}$)2 | ||
| C. | f(x)=cosx•tanx,g(x)=sinx | D. | f(x)=x2,g(x)=$\sqrt{{x}^{4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | -$\frac{3\sqrt{2}}{4}$ | D. | $\frac{3\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{3}{2}$] | B. | (-∞,4] | C. | [$\frac{3}{2}$,2] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com