
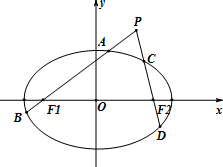
 ��ͼ����֪��Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2��������Ϊ$\frac{{\sqrt{2}}}{2}$�������ĸ��������ɵ����ε����Ϊ8$\sqrt{2}$��������P������x���ϣ���ֱ��PF1��PF2����Բ�Ľ���ֱ�ΪA��B��C��D��
��ͼ����֪��Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2��������Ϊ$\frac{{\sqrt{2}}}{2}$�������ĸ��������ɵ����ε����Ϊ8$\sqrt{2}$��������P������x���ϣ���ֱ��PF1��PF2����Բ�Ľ���ֱ�ΪA��B��C��D������ ��1��ֱ�Ӽ��㼴�ý��ۣ�
��2����ֱ��PF2��б�ʴ����벻��������������ۼ��ɣ�
��� �⣺�⣺��1����S=2ab=8$\sqrt{2}$��e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$����a��b��0��
��a=2$\sqrt{2}$��b=c=2��
���������Բ����Ϊ��$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1��
��2�����ۣ������������ĵ�P��ʹ��|AB|=2|CD|������
�������£�
��|AB|=2|CD|��������P����y����Ҳ࣬
��ֱ��PF1�ش�����Ϊk1��
��ֱ��PF2��б�ʴ���ʱ��Ϊk2��
��ʱ��ֱ��PF1��y=k1��x+2������$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1��
��ȥy�����ã���1+2k12��x2+8k12x+8��k12-1��=0
ֱ��PF1Ϊ��y=k1��x+2����ֱ��PF2Ϊ��y=k2��x-2����
��Τ�ﶨ������x1+x2=-$\frac{8{k}_{1}^{2}}{1+2{k}_{1}^{2}}$��${x}_{1}{x}_{2}=\frac{8��{k}_{1}^{2}-1��}{1+2{k}_{1}^{2}}$
��$|AB|=\sqrt{1+{k}_{1}^{2}}•\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{1+{k}_{1}^{2}}•\sqrt{��\frac{-8{k}_{1}^{2}}{1+2{k}_{1}^{2}}��^{2}-4•\frac{8��{k}_{1}^{2}-1��}{1+2{k}_{1}^{2}}}$
=4$\sqrt{2}•\frac{1+{k}_{1}^{2}}{1+2{k}_{1}^{2}}$
ͬ���ɵ�|CD|=4$\sqrt{2}•\frac{1+{k}_{2}^{2}}{1+2{k}_{2}^{2}}$
��|AB|=2|CD����������$\frac{1+{k}_{1}^{2}}{1+2{k}_{1}^{2}}=2•\frac{1+{k}_{2}^{2}}{1+2{k}_{2}^{2}}$
�����ã�2k12k22+3k12+1=0��
��Ϊ�˷�����ʵ���⣬���Բ����������ĵ�P��ʹ��|AB|=2|CD|������
��ֱ��PF2��б�ʲ�����ʱ��|CD|=$\frac{2{b}^{2}}{a}$=2$\sqrt{2}$��
��ʱ|AB|=2|CD|=4$\sqrt{2}$=2a��������
���Ͽɵã������������ĵ�P��ʹ��|AB|=2|CD|������
���� ���⿼����Բ�ļ����ʣ������������������ע����ⷽ���Ļ��ۣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ƽ�� | B�� | ��ֱ | C�� | ���� | D�� | �ཻ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.22 | B�� | 0.28 | C�� | 0.36 | D�� | 0.64 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | g��x��=sin2x+2 | B�� | g��x��=sin��2x+$\frac{��}{6}$��+2 | C�� | g��x��=sin��2x+$\frac{��}{6}$��+1 | D�� | g��x��=sin��4x-$\frac{��}{3}$��+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1��0��-1��0���� | B�� | 1��11��111��1111���� | C�� | 1��5��9��13���� | D�� | 1��2��4��8���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com