
分析 (1)由分段数列,分别求得a2,a3,a4,…,即可得到n为偶数时,奇数时的通项;
(2)运用分组求和,以及等差数列和等比数列的求和公式,计算比较,即可得到最大值.
解答 解:(1)a1=10,an=$\left\{\begin{array}{l}{{2}^{{a}_{n-1}},n=2k}\\{-1+lo{g}_{2}{a}_{n-1},n=2k+1}\end{array}\right.$(k∈N*),
可得a2=2a1=210;a3=-1+log2a2=-1+log2210=-1+10=9;
a4=2a3=29;a5=-1+log2a4=-1+9=8;
…,an=${2}^{11-\frac{n}{2}}$(n为偶数),an=$\frac{21-n}{2}$(n为奇数).
当n为偶数时,n-1为奇数,an=${2}^{\frac{21-(n-1)}{2}}$,
当n为奇数时,n-1为偶数,an=-1+log2${2}^{11-\frac{n-1}{2}}$=10-$\frac{1+n}{2}$,
则有{an}的通项公式为an=$\left\{\begin{array}{l}{\frac{21-n}{2},n为奇数}\\{{2}^{11-\frac{n}{2}},n为偶数}\end{array}\right.$;
(2)当n为偶数时,Sn=(10+9+…+$\frac{21-n}{2}$)+(210+29+…+${2}^{11-\frac{n}{2}}$)
=$\frac{n}{2}$•10+$\frac{1}{2}•$$\frac{n}{2}$•($\frac{n}{2}$-1)•(-1)+$\frac{{2}^{10}(1-\frac{1}{{2}^{\frac{n}{2}}})}{1-\frac{1}{2}}$
=-$\frac{1}{8}$(n2-42n)+211-${2}^{11-\frac{n}{2}}$,
则Sn+1=Sn+$\frac{21-(n+1)}{2}$=Sn+$\frac{20-n}{2}$,
当n为奇数时,Sn+1=Sn+${2}^{\frac{21-n}{2}}$,
即有S1<S2<S3<…<S20=S21<S22>S23>…
则S22取得最大值,且为-$\frac{1}{8}$(222-42×22)+211-1=2102.
点评 本题考查分段数列的运用,主要考查等差数列和等比数列的通项公式和求和公式的运用,考查运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
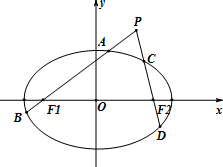 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com