
分析 已知等式利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式变形,根据sinA不为0求出cosB的值,由D为边AC的中点,可得2$\overrightarrow{BD}$=$\overrightarrow{BA}$+$\overrightarrow{BC}$,两边平方,设|$\overrightarrow{BA}$|=c,|$\overrightarrow{BC}$|=a,可得4=a2+c2+$\frac{2}{3}$ac,结合基本不等式的应用可得ac的最大值,利用三角形面积公式即可得解.
解答  解:∵bcosC=(3a-c)cosB,
解:∵bcosC=(3a-c)cosB,
∴利用正弦定理化简得:(3sinA-sinC)cosB=sinBcosC,
整理得:3sinAcosB=sinBcosC+cosBsinC=sin(B+C)=sinA,
∵sinA≠0,
∴cosB=$\frac{1}{3}$,可得sinB=$\frac{2\sqrt{2}}{3}$,
∵点D为边AC的中点,
∴2$\overrightarrow{BD}$=$\overrightarrow{BA}$+$\overrightarrow{BC}$,
∴两边平方可得:4|$\overrightarrow{BD}$|2=|$\overrightarrow{BA}$|2+2|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|•cos∠ABC+|$\overrightarrow{BC}$|2,…(9分)
设|$\overrightarrow{BA}$|=c,|$\overrightarrow{BC}$|=a,可得:4=a2+c2+$\frac{2}{3}$ac≥ac,(当且仅当a=c=2时等号成立),
∴ac≤$\frac{3}{2}$,(当且仅当a=c=2时等号成立),
∴S△ABC=$\frac{1}{2}$acsin∠ABC≤$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2\sqrt{2}}{3}$=$\frac{\sqrt{2}}{2}$(当且仅当a=c=2时等号成立),
∴S△ABD=$\frac{1}{2}$S△ABC=$\frac{{\sqrt{2}}}{4}$.(当且仅当a=c=2时等号成立),
∴当且仅当a=c=2时,△ABD面积的最大值为$\frac{{\sqrt{2}}}{4}$.…(12分)
点评 本题主要考查了正弦定理,三角形内角和定理,三角函数恒等变换的应用,考查了平面向量及其应用,考查了基本不等式,三角形面积公式等知识在解三角形中的应用,考查了转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
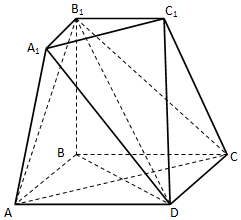 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,1+\frac{1}{e}})$ | B. | $({1,1+\frac{1}{e}})$ | C. | (1,1+e) | D. | (1,1+e2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com