
如图,一简单几何体的一个面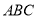 内接于圆
内接于圆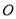 ,
,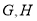 分别是
分别是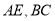 的中点,
的中点,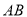 是圆
是圆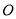 的直径,四边形
的直径,四边形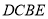 为平行四边形,且
为平行四边形,且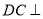 平面
平面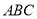 .
.
(1)求证: 平面
平面 ;
;
(2)若AC=BC=BE=2,求二面角O-CE-B的余弦值.
(1)证明见解析;(2) .
.
【解析】
试题分析:(1)证明线面垂直需通过证明面面垂直,根据题意 分别是
分别是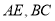 的中点,连接
的中点,连接 ,利用三角形的中位线性质,易证:平面
,利用三角形的中位线性质,易证:平面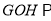 平面
平面 ;(2)根据题意可知
;(2)根据题意可知 两两垂直,可以
两两垂直,可以 为原点,分别以
为原点,分别以 为
为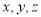 轴建立空间直角坐标系,找到
轴建立空间直角坐标系,找到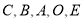 的坐标,显然平面
的坐标,显然平面 的法向量为
的法向量为 ,而平面
,而平面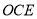 的法向量设为:
的法向量设为: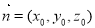 利用
利用 ,求得其中一个法向量,于是二面角的余弦值利用公式即可得到.
,求得其中一个法向量,于是二面角的余弦值利用公式即可得到.
试题解析:(1)证明:连结
∵
∴ 平面
平面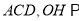 平面
平面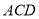 ,又
,又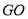 交
交 于
于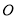
∴平面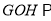 平面
平面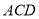
∴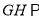 平面
平面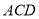
法一:以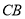 为
为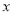 轴,
轴,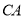 为
为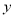 轴,
轴, 为
为 轴,建立如图所示的直角坐标系
轴,建立如图所示的直角坐标系
则C(0,0,0),B(2,0,0),A(0,2,0),O(1,1,0),E(2,0,2)
平面BCE的法向量 ,设平面OCE的法向量
,设平面OCE的法向量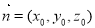
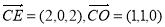
∴ 则
则 ,故
,故
令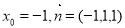
∵二面角O-CE-B是锐二面角,记为 ,则
,则
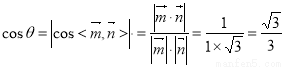
法二:过H作HM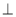 CE于M,连结OM
CE于M,连结OM
∵DC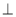 平面ABC ∴平面BCDE
平面ABC ∴平面BCDE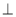 平面ABC
平面ABC
又∵AB是圆O的直径 ∴AC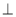 BC,而AC//OH
BC,而AC//OH
∴OH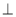 BC ∴OH
BC ∴OH 平面BCE
平面BCE
∴OH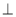 CE ,又HM
CE ,又HM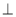 CE于M ∴CE
CE于M ∴CE 平面OHM
平面OHM
∴CE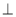 OM ∴
OM ∴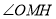 是二面角O-CE-B的平面角
是二面角O-CE-B的平面角
由 且CE=
且CE=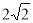 . ∴
. ∴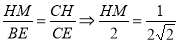
∴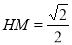 又OH=
又OH=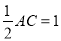
在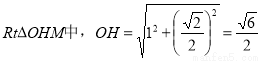 .
.
∴
考点:1.线面平行的判定定理;2.空间向量求二面角.


科目:高中数学 来源:2014-2015学年豫晋冀高三上学期第二次调研考试理科数学试卷(解析版) 题型:选择题
已知向量 ,且
,且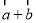 与
与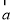 共线,那么
共线,那么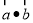 的值为( )
的值为( )
A .l B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省宜宾市高三第一次诊断考试文科数学试卷(解析版) 题型:选择题
在平面直角坐标系中,椭圆 的焦距为
的焦距为 ,以
,以 为圆心,
为圆心,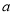 为半径作圆,过点
为半径作圆,过点 作圆的两条切线互相垂直,则离心率
作圆的两条切线互相垂直,则离心率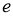 为 ( )
为 ( )
(A) (B)
(B) (C)
(C) (D)
(D)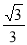
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省宜宾市高三第一次诊断考试文科数学试卷(解析版) 题型:选择题
抛物线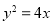 的焦点坐标是( )
的焦点坐标是( )
(A)(0,1) (B)(0,-1) (C)(-1,0) (D) (1,0)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省宜宾市高三第一次诊断考试理科数学试卷(解析版) 题型:选择题
顶点在原点,对称轴为坐标轴,且过点 的抛物线的标准方程是( )
的抛物线的标准方程是( )
(A)
(B)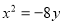
(C) 或
或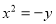
(D) 或
或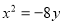
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三一诊模拟文科数学试卷(解析版) 题型:选择题
已知函数 对定义域
对定义域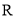 内的任意
内的任意 都有
都有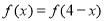 ,且当
,且当 时,其导函数
时,其导函数
满足 ,若
,若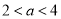 ,则( )
,则( )
A.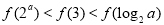
B.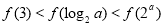
C.
D.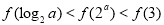
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com