
分析 由已知可得$\frac{2sinC}{sinA}=\frac{sinB}{sinA}+\frac{cosB}{cosA}$,进一步得到sinC=2sinCcosA,求得cosA=$\frac{1}{2}$,结合A的范围得答案.
解答 解:由$\frac{sinB}{sinA}$,$\frac{sinC}{sinA}$,$\frac{cosB}{cosA}$成等差数列,
得$\frac{2sinC}{sinA}=\frac{sinB}{sinA}+\frac{cosB}{cosA}$,
∴sinBcosA+cosBsinA═2sinCcosA,得sin(B+A)=sinC=2sinCcosA,
∴cosA=$\frac{1}{2}$,
∵0<A<π,∴A=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查等差数列的通项公式,考查三角函数的化简求值,是中档题.


科目:高中数学 来源: 题型:选择题
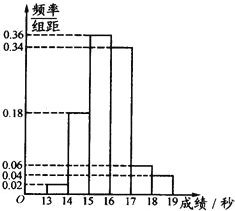 某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,如图是测试成绩频率分布直方图.成绩小于17秒的学生人数为( )
某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,如图是测试成绩频率分布直方图.成绩小于17秒的学生人数为( )| A. | 45 | B. | 35 | C. | 17 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄态度 | 支持 | 不支持 |
| 20岁以上50岁以下 | 800 | 200 |
| 50岁以上(含50岁) | 100 | 300 |
| P(K2≥k0) | 0.05 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10000001110(2) | B. | 10000011110(2) | C. | 100000011101(2) | D. | 10000001100(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(kπ,kπ+\frac{π}{4})$ | B. | $(2kπ,2kπ+\frac{π}{2})$ | C. | $[kπ+\frac{π}{4},kπ+\frac{π}{2})$ | D. | 以上都不对.(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com