
分析 根据新定义,将关于x的不等式:(x-a)?(x+1-a)>0转化为一般不等式,然后解之,利用集合的关系得到所求.
解答 解:由已知新定义得到关于x的不等式:(x-a)?(x+1-a)>0为$\frac{x-a}{1+a-x}>0$即$\frac{x-a}{x-a-1}<0$,所以不等式的解集为:{x|a<x<a+1},此集合为集合{x|-2≤x≤2}的子集,
所以$\left\{\begin{array}{l}{a≥-2}\\{a+1≤2}\end{array}\right.$,解得-2≤a≤1,则实数a的取值范围是[-2,1];
故答案为:[-2,1].
点评 本题考查了分式不等式的解法;关键是正确根据新定义将不等式化为常见的分式不等式解之;根据集合关系求参数范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (C${\;}_{8}^{3}$+C${\;}_{7}^{2}$)(C${\;}_{7}^{3}$+C${\;}_{8}^{2}$) | B. | (C${\;}_{8}^{3}$+C${\;}_{7}^{2}$)+(C${\;}_{7}^{3}$+C${\;}_{8}^{2}$) | ||
| C. | C${\;}_{8}^{3}$C${\;}_{7}^{2}$+C${\;}_{7}^{3}$C${\;}_{8}^{2}$ | D. | C${\;}_{8}^{3}$C${\;}_{7}^{2}$+C${\;}_{7}^{3}$+C${\;}_{11}^{1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
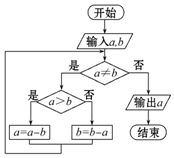 某同学根据“更相减损术”设计出程序框图(图).若输入a的值为98,b的值为63,则执行该程序框图输出的结果为( )
某同学根据“更相减损术”设计出程序框图(图).若输入a的值为98,b的值为63,则执行该程序框图输出的结果为( )| A. | 0 | B. | 7 | C. | 14 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
| 平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
| 用电量(万度) | 38 | 35 | 41 | 36 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com