
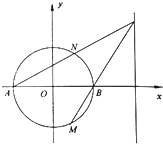
 已知圆O:x2+y2=4交x轴于A,B两点,点P是直线x=4上一点,直线PA,PB分别交圆O于点N,M.
已知圆O:x2+y2=4交x轴于A,B两点,点P是直线x=4上一点,直线PA,PB分别交圆O于点N,M.分析 (1)写出直线AN的方程,求出点P的坐标,写出直线BP的方程,由直线BP与圆的方程组成方程组求出点M的坐标;
(2)设出点P,写出直线AN的方程,与圆的方程联立求出点N的坐标,写出直线BM的方程,与圆的方程联立求出点M的坐标,从而求出直线MN过定点.
解答 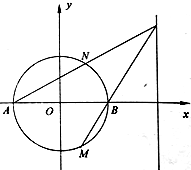 解:(1)因为点N(0,2),A(-2,0),
解:(1)因为点N(0,2),A(-2,0),
所以直线AN的方程为y=x+2,
令x=4,则P(4,6),
又因为B(2,0),
所以直线BP的方程为y=3(x-2),
由y=3(x-2)及x2+y2=4,
解得$M(\frac{8}{5},-\frac{6}{5})$;
(2)设P(4,t),因为点A(-2,0),
所以直线AN的方程为$y=\frac{t}{6}(x+2)$,
由$y=\frac{t}{6}(x+2)$及x2+y2=4,解得$N(\frac{{72-2{t^2}}}{{36+{t^2}}},\frac{24t}{{36+{t^2}}})$,
因为点B(2,0),所以直线BM的方程为$y=\frac{t}{2}(x-2)$,
由$y=\frac{t}{2}(x-2)$及x2+y2=4,解得$M(\frac{{2{t^2}-8}}{{4+{t^2}}},\frac{-8t}{{4+{t^2}}})$,
过定点C(1,0),因为${k_{NC}}=\frac{{\frac{24t}{{36+{t^2}}}}}{{\frac{{72-2{t^2}}}{{36+{t^2}}}-1}}=\frac{8t}{{12-{t^2}}}$,
${k_{MC}}=\frac{{\frac{-8t}{{4+{t^2}}}}}{{\frac{{2{t^2}-8}}{{4+{t^2}}}-1}}=\frac{-8t}{{{t^2}-12}}$,
所以kNC=kMC,
所以M,N,C三点共线,
所以直线MN恒过定点C(1,0).
点评 本题考查了直线与圆的方程的应用问题,也考查了直线过定点的判断问题,考查了数形结合思想的应用问题,是综合性题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com