
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{7}$ |
分析 由题意可得A、B两点在直线y=$\frac{1}{3}$x上的同侧,求得A关于直线的对称点M的坐标,故当点C为直线BM和直线y=$\frac{1}{3}$x的交点时,|AC|+|BC|的最小值为|BM|.
解答 解:由题意A、B两点在直线y=$\frac{1}{3}$x的同侧.
设A关于直线y=$\frac{1}{3}$x的对称点M的坐标为(a,b),则$\left\{\begin{array}{l}{\frac{b-1}{a+2}•\frac{1}{3}=-1}\\{\frac{1+b}{2}=\frac{1}{3}•\frac{a-2}{2}}\end{array}\right.$,
解得a=-1,b=-2
∴A关于直线的对称点M的坐标为(-1,-2),
故当点C为直线BM和直线y=$\frac{1}{3}$x的交点时,|AC|+|BC|的最小值为|BM|=$\sqrt{(1+1)^{2}+(2+2)^{2}}$=2$\sqrt{5}$,
故选:C.
点评 本题主要考查求一个点关于直线的对称点的坐标,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $(\sqrt{3},1)$ | B. | $(1,\sqrt{3})$ | C. | $(\frac{{\sqrt{3}}}{2},\frac{1}{2})$ | D. | $(\frac{1}{2},\frac{{\sqrt{3}}}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
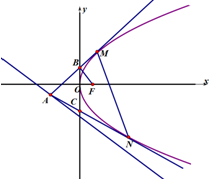 过直线x+2y+5=0上一动点A(A不在y轴上)作焦点为F(2,0)的抛物线y2=2px的两条切线,M,N为切点,直线AM,AN分别与y轴交于点B,C.
过直线x+2y+5=0上一动点A(A不在y轴上)作焦点为F(2,0)的抛物线y2=2px的两条切线,M,N为切点,直线AM,AN分别与y轴交于点B,C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{6}{5}$ | C. | 3 | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
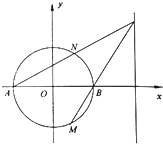 已知圆O:x2+y2=4交x轴于A,B两点,点P是直线x=4上一点,直线PA,PB分别交圆O于点N,M.
已知圆O:x2+y2=4交x轴于A,B两点,点P是直线x=4上一点,直线PA,PB分别交圆O于点N,M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平面α∥平面β,过点P的两条斜线分别交平面α、β于A、C及B、D.点P在平面α内的射影0点在线段AB上,且PA=8,AB=5,PB=7,CD=20.求:
如图,平面α∥平面β,过点P的两条斜线分别交平面α、β于A、C及B、D.点P在平面α内的射影0点在线段AB上,且PA=8,AB=5,PB=7,CD=20.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com