
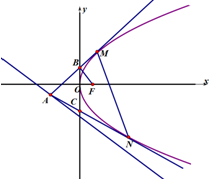
 过直线x+2y+5=0上一动点A(A不在y轴上)作焦点为F(2,0)的抛物线y2=2px的两条切线,M,N为切点,直线AM,AN分别与y轴交于点B,C.
过直线x+2y+5=0上一动点A(A不在y轴上)作焦点为F(2,0)的抛物线y2=2px的两条切线,M,N为切点,直线AM,AN分别与y轴交于点B,C.分析 ( I ) 利用抛物线的焦点,可得P=4,求出抛物线y2=8x.设B(0,b),则直线AM为y=k1x+b,与抛物线y2=8x联立,利用判别式为0,推出k1kBF=-1..即BF⊥AM,同理:CF⊥AN,AF为△ABC的外接圆直径,求解△ABC的外接圆面积最小值.
(Ⅱ)设点A(x0,y0),M(x1,y1),N(x2,y2),求出直线AM方程,直线MN方程,通过点A(x0,y0)满足:x0+2y0+5=0,推出直线MN恒过定点.
解答 证明:( I ) 焦点为F(2,0)的抛物线y2=2px,可得P=4,抛物线y2=8x.
设B(0,b),则直线AM为y=k1x+b,与抛物线y2=8x联立,得:k12x2+2(2k1b-8)x+b2=0.
因为相切,所以${△_1}={(2{k_1}b-8)^2}-4k_1^2{b^2}=0$,得:${k_1}=\frac{2}{b}$,又${k_{BF}}=\frac{b-0}{0-2}=-\frac{b}{2}$,所以k1kBF=-1.
即BF⊥AM,同理:CF⊥AN,所以AF为△ABC的外接圆的直径,
又因为:${|{AF}|_{min}}=\frac{7}{{\sqrt{5}}}$,
所以△ABC的外接圆面积最小值为:$\frac{49}{20}π$
(Ⅱ)设点A(x0,y0),M(x1,y1),N(x2,y2),
易知:直线AM方程为:4x-y1y+4x1=0,
代入点A坐标得:4x0-y1y0+4x1=0,同理:4x0-y2y0+4x2=0,
所以直线MN方程为:4x-y0y+4x0=0,又点A(x0,y0)满足:x0+2y0+5=0
所以直线MN恒过定点(5,-8)
点评 本题考查抛物线方程的求法,直线与抛物线位置关系的综合应用,考查转化思想以及计算能力.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:选择题
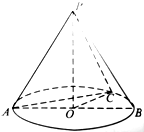 如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$的中点,则二面角B-PA-C的余弦值为( )
如图,在圆锥PO中,已知PO=$\sqrt{2}$,⊙O的直径AB=2,C是$\widehat{AB}$的中点,则二面角B-PA-C的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{15}}{5}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
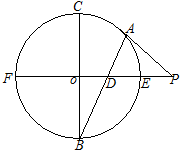 如图,直线PA为⊙O的切线,切点为A,PO交⊙O于E,F两点,直径BC⊥OP,连接AB交PO于点D.
如图,直线PA为⊙O的切线,切点为A,PO交⊙O于E,F两点,直径BC⊥OP,连接AB交PO于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 三棱锥A-BCD中,面ABC⊥底面BCD,∠BAC=90°,AB=AC,∠BCD=90°,∠BDC=60°,BC=2a.
三棱锥A-BCD中,面ABC⊥底面BCD,∠BAC=90°,AB=AC,∠BCD=90°,∠BDC=60°,BC=2a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com