
分析 (Ⅰ)求出函数的导数,可得切线的斜率和切点,由点斜式方程可得切线的方程;
(Ⅱ)假设存在实数m满足题意,则不等式$lnx+\frac{m}{x}<\frac{e^x}{x}$对$x∈(\frac{1}{2},+∞)$恒成立.即m<ex-xlnx对$x∈(\frac{1}{2},+∞)$恒成立.令h(x)=ex-xlnx,求出导数,令φ(x)=ex-lnx-1,求出导数,运用函数存在定理,结合基本不等式可得最值,进而得到m的范围和最大整数.
解答 解:(Ⅰ)因为函数f(x)=lnx的导数$f'(x)=\frac{1}{x}$,
所以f′(1)=1,则所求切线的斜率为1,
又f(1)=ln1=0,
故所求切线的方程为y=x-1;
(Ⅱ)假设存在实数m满足题意,
则不等式$lnx+\frac{m}{x}<\frac{e^x}{x}$对$x∈(\frac{1}{2},+∞)$恒成立.
即m<ex-xlnx对$x∈(\frac{1}{2},+∞)$恒成立.
令h(x)=ex-xlnx,则h'(x)=ex-lnx-1,
令φ(x)=ex-lnx-1,则$φ'(x)={e^x}-\frac{1}{x}$,
因为φ'(x)在$(\frac{1}{2},+∞)$上单调递增,
$φ'(\frac{1}{2})={e^{\frac{1}{2}}}-2<0$,φ'(1)=e-1>0,
且φ'(x)的图象在$(\frac{1}{2},1)$上连续,
所以存在${x_0}∈(\frac{1}{2},1)$,使得φ'(x0)=0,即${e^{x_0}}-\frac{1}{x_0}=0$,
则x0=-lnx0,
所以当x∈($\frac{1}{2}$,x0)时,φ(x)单调递减;
当x∈(x0,+∞)时,φ(x)单调递增,
则φ(x)取到最小值φ(x0)=${e}^{{x}_{0}}$-lnx0-1=x0+$\frac{1}{{x}_{0}}$-1≥2$\sqrt{{x}_{0}•\frac{1}{{x}_{0}}}$-1=1>0,
所以h′(x)>0,即h(x)在区间($\frac{1}{2}$,+∞)内单调递增.
所以m≤h($\frac{1}{2}$)=e${\;}^{\frac{1}{2}}$-$\frac{1}{2}$ln$\frac{1}{2}$=e${\;}^{\frac{1}{2}}$+$\frac{1}{2}$ln2=1.99525,
所以存在实数m满足题意,且最大整数m的值为1.
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查任意性和存在性问题的解法,注意运用转化思想和构造函数法,求出导数判断单调性,考查化简整理的运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
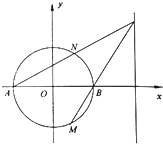 已知圆O:x2+y2=4交x轴于A,B两点,点P是直线x=4上一点,直线PA,PB分别交圆O于点N,M.
已知圆O:x2+y2=4交x轴于A,B两点,点P是直线x=4上一点,直线PA,PB分别交圆O于点N,M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,有一个边长为2的正方形,其中有一块边长为1的阴影部分,向大的正方形中撒芝麻,假设芝麻落在正方形中任何位置上的概率相等,则芝麻落在阴影区域上的概率为$\frac{1}{4}$.
如图,有一个边长为2的正方形,其中有一块边长为1的阴影部分,向大的正方形中撒芝麻,假设芝麻落在正方形中任何位置上的概率相等,则芝麻落在阴影区域上的概率为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平面α∥平面β,过点P的两条斜线分别交平面α、β于A、C及B、D.点P在平面α内的射影0点在线段AB上,且PA=8,AB=5,PB=7,CD=20.求:
如图,平面α∥平面β,过点P的两条斜线分别交平面α、β于A、C及B、D.点P在平面α内的射影0点在线段AB上,且PA=8,AB=5,PB=7,CD=20.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com