
分析 曲线C:$\left\{\begin{array}{l}{x=-2+cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数,0≤θ<2π)化为(x+2)2+y2=1,设$\frac{y}{x}$=k,即kx-y=0,利用直线与圆的位置关系即可得出.
解答 解:曲线C:$\left\{\begin{array}{l}{x=-2+cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数,0≤θ<2π)化为(x+2)2+y2=1,表示以(-2,0)为圆心,1为半径的圆.
设$\frac{y}{x}$=k,即kx-y=0,
则$\frac{|-2k|}{\sqrt{1+{k}^{2}}}$≤1,化为:${k}^{2}≤\frac{1}{3}$,解得$-\frac{\sqrt{3}}{3}$≤k$≤\frac{\sqrt{3}}{3}$.
故答案为:$[-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3}]$.
点评 本题考查了参数方程化为普通方程、点到直线的距离公式、不等式的解法、直线与圆的位置关系,考查了推理能力与计算能力,属于中档题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
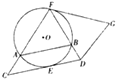 如图所示,CD,GF为圆O的两条切线,其中E,F分别为圆O的两个切点,∠FCD=∠DFG.
如图所示,CD,GF为圆O的两条切线,其中E,F分别为圆O的两个切点,∠FCD=∠DFG.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
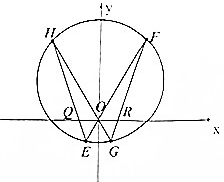 已知圆C的周长被y轴平分,且经过点A($\sqrt{3}$,0),B(0,3).
已知圆C的周长被y轴平分,且经过点A($\sqrt{3}$,0),B(0,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com