
分析 以P为原点,PA为x轴,PB为y轴,PC为z轴,建立空间直角坐标系,利用向量法能求出M到三棱锥三个侧面的距离的平方和的最小值.
解答 解:以P为原点,PA为x轴,PB为y轴,PC为z轴,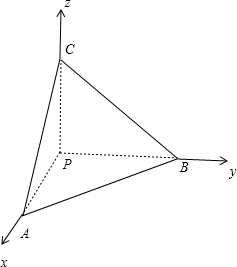
建立空间直角坐标系,
由已知得A(3,0,0),B(0,3,0),C(0,0,4),
∴平面ABC为:$\frac{1}{3}x+\frac{1}{3}y+\frac{1}{4}z$=1,
∴1=($\frac{1}{3}x+\frac{1}{3}y+\frac{1}{4}z$)2≤[($\frac{1}{3}$)2+($\frac{1}{3}$)2+($\frac{1}{4}$)2](x2+y2+z2),
解得x2+y2+z2≥$\frac{144}{41}$.
又M是底面ABC内一点,
∴M到三棱锥三个侧面的距离的平方和的最小值是$\frac{144}{41}$.
故答案为:$\frac{144}{41}$.
点评 本题考查点到三棱锥三个侧面的距离的平方和的最小值的求法,是中档题,解题时要注意向量法的合理运用.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:填空题
 如图,有一个边长为2的正方形,其中有一块边长为1的阴影部分,向大的正方形中撒芝麻,假设芝麻落在正方形中任何位置上的概率相等,则芝麻落在阴影区域上的概率为$\frac{1}{4}$.
如图,有一个边长为2的正方形,其中有一块边长为1的阴影部分,向大的正方形中撒芝麻,假设芝麻落在正方形中任何位置上的概率相等,则芝麻落在阴影区域上的概率为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com