
分析 (1)解法一:当a=-1时,不等式即|x+$\frac{1}{2}$|-|x-$\frac{1}{2}$|≤$\frac{1}{2}$,再利用绝对值的意义求得不等式f(x)≤|2x-1|的解集.
解法二:把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(2)由条件|2x-a|+a≤2,利用绝对值三角不等式证得|x|≤1,从而证得结论.
解答 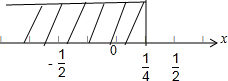 解:(1)解法一:当a=-1时,解不等式f(x)≤|2x-1|,
解:(1)解法一:当a=-1时,解不等式f(x)≤|2x-1|,
即|2x+1|-1≤|2x-1|,即|x+$\frac{1}{2}$|-|x-$\frac{1}{2}$|≤$\frac{1}{2}$.
而|x+$\frac{1}{2}$|-|x-$\frac{1}{2}$|表示数轴上的x对应点到-$\frac{1}{2}$对应点的距离
减去它到$\frac{1}{2}$对应点的距离,
而$\frac{1}{4}$对应点到-$\frac{1}{2}$对应点的距离减去它到$\frac{1}{2}$对应点的距离正好等于$\frac{1}{2}$,
故不等式f(x)≤|2x-1|的解集为{x|x≤$\frac{1}{4}$}.
解法二:不等式f(x)≤|2x-1|,即|2x+1|-|2x-1|≤1,
∴$\left\{\begin{array}{l}{x<-\frac{1}{2}}\\{-2x-1-(1-2x)≤1}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{-\frac{1}{2}≤x<\frac{1}{2}}\\{2x+1-(1-2x)≤1}\end{array}\right.$②,或$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{2x+1-(2x-1)≤1}\end{array}\right.$③.
解①求得x<-$\frac{1}{2}$,解②求得-$\frac{1}{2}$≤x≤$\frac{1}{4}$,解求得x∈∅.
综上可得,不等式f(x)≤|2x-1|的解集为{x|x≤$\frac{1}{4}$}.
(2)证明:∵f(x)=|2x-a|+a≤2,而由绝对值三角不等式可得|2x-a|≥|2x|-|a|=|2x|-a,
∴|2x|-a+a≤2,即 2|x|≤2,即|x|≤1.
又∵a≥0,∴|x|≤a+1成立.
点评 本题主要考查绝对值的意义,绝对值三角不等式的应用,体现了转化、分类讨论的数学思想,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,$\frac{3π}{4}$) | B. | (2$\sqrt{3}$,$\frac{3π}{4}$) | C. | (2$\sqrt{3}$,π) | D. | (3,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆C的周长被y轴平分,且经过点A($\sqrt{3}$,0),B(0,3).
已知圆C的周长被y轴平分,且经过点A($\sqrt{3}$,0),B(0,3).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2a | B. | 2-a-1 | C. | 1-2-a | D. | 2a-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com