
分析 说明顶点A1 在平面 ABC 上的射影为△ABC 的外心,通过数据关系求出几何体的侧面积.
解答 解:∵A1A=A1B=A1C
∴点 A1 在平面 ABC 上的射影为△ABC 的外心,在∠BAC 平分线 AD 上
∵AB=AC
∴AD⊥BC
∵AD 为 A1A 在平面 ABC 上的射影
∴BC⊥AA1
∴BC⊥BB1
∴BB1C1C 为矩形,S=BB1×BC=156 取BC中点 E,连 A1E 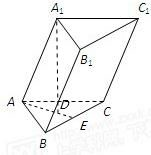
∵A1A=A1B
∴A1E⊥AB
∴A1E=12
∴SAA1C1C=SAA1B1B=120
∴S侧=396.
这个棱柱的全面积为:396.
点评 本题考查棱柱的侧面积,考查空间想象能力,逻辑推理计算能力,点 A1 在平面 ABC 上的射影为△ABC 的外心,在∠BAC 平分线 AD 上,是解题的关键;是基础题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
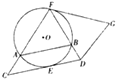 如图所示,CD,GF为圆O的两条切线,其中E,F分别为圆O的两个切点,∠FCD=∠DFG.
如图所示,CD,GF为圆O的两条切线,其中E,F分别为圆O的两个切点,∠FCD=∠DFG.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{4+\frac{π^2}{9}}$ | C. | $\sqrt{1+\frac{π^2}{9}}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,$\frac{3π}{4}$) | B. | (2$\sqrt{3}$,$\frac{3π}{4}$) | C. | (2$\sqrt{3}$,π) | D. | (3,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2a | B. | 2-a-1 | C. | 1-2-a | D. | 2a-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com