
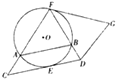
 如图所示,CD,GF为圆O的两条切线,其中E,F分别为圆O的两个切点,∠FCD=∠DFG.
如图所示,CD,GF为圆O的两条切线,其中E,F分别为圆O的两个切点,∠FCD=∠DFG.分析 (1)利用弦切角定理,结合条件,即可证明:AB∥CD;
(2)连接AE,FE,利用弦切角定理、正弦定理证明:$\frac{ED}{EC}$=$\frac{BD}{AC}$.
解答 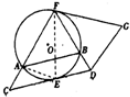 (1)证明:由题意,∠FAB=∠DFG,
(1)证明:由题意,∠FAB=∠DFG,
∵∠FCD=∠DFC,
∴∠FCD=∠FAB,
∴AB∥CD;
(2)解:连接AE,FE,
∵CD切圆O于点E,
∴∠CEA=∠AFE,
∵AB∥CD,
∴∠CEA=∠EAB,
∵∠EFD=∠EAB,
∴∠EFD=∠AFE.
△EFD中,由正弦定理可得$\frac{ED}{sin∠EFD}$=$\frac{FD}{sin∠FED}$.
△EFC中,由正弦定理可得$\frac{EC}{sin∠AFE}$=$\frac{FC}{sin∠FEC}$,
∵∠FEC=π-∠FED,
∴$\frac{ED}{EC}$=$\frac{FD}{FC}$,
∵AB∥CD,
∴$\frac{BD}{AC}$=$\frac{FD}{FC}$,
∴$\frac{ED}{EC}$=$\frac{BD}{AC}$.
点评 本题考查弦切角定理、正弦定理,考查学生分析解决问题的能力,正确运用弦切角定理、正弦定理是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平面α∥平面β,过点P的两条斜线分别交平面α、β于A、C及B、D.点P在平面α内的射影0点在线段AB上,且PA=8,AB=5,PB=7,CD=20.求:
如图,平面α∥平面β,过点P的两条斜线分别交平面α、β于A、C及B、D.点P在平面α内的射影0点在线段AB上,且PA=8,AB=5,PB=7,CD=20.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com