
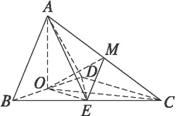
(1)求证:AO⊥平面BCD;
(2)求异面直线AB与CD所成角的大小;
(3)求点E到平面ACD的距离.
解法1:(1)证明:连结OC.
∵BO=DO,AB=AD,∴AO⊥BD.
∵BO=DO,BC=CD,∴CO⊥BD.
在△AOC中,由已知可得AO=1,CO=![]() ,
,
而AC=2,
∴AO2+CO2=AC2.
∴∠AOC=90°,即AO⊥OC.
∵BD∩OC=O,∴AO⊥平面BCD.

(2)解:取AC的中点M,连结OM,ME,OE,
由E为BC的中点知ME∥AB,OE∥DC.
∴直线OE与EM所成的锐角就是异面直线AB与CD所成的角.
在△OME中,
EM=![]() AB=
AB=![]() ,OE=
,OE=![]() DC=1,
DC=1,
∵OM是Rt△AOC斜边AC上的中线,
∴OM=![]() AC=1.
AC=1.
∴cosOEM=![]() .
.
∴异面直线AB与CD所成角的大小为arccos![]() .
.
(3)解:设点E到平面ACD的距离为h.
∵V E—ACD=V A—CDE,
∴![]() h·S△ACD=
h·S△ACD=![]() ·AO·S△CDE.
·AO·S△CDE.
在△ACD中,CA=CD=2,AD=![]() ,
,
∴S△ACD=![]() ×
×![]() ×
×![]() .
.
而AO=1,S△CDE=![]() ×
×![]() ×22=
×22=![]() ,
,
∴h= .
.
∴点E到平面ACD的距离为![]() .
.
解法2:(1)同解法1.
(2)解:如下图,以O为原点,建立空间直角坐标系,
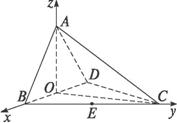
则B(1,0,0),D(-1,0,0),C(0,![]() ,0),A(0,0,1),E(
,0),A(0,0,1),E(![]() ,
,![]() ,0),
,0),![]() =(-1,0,1),
=(-1,0,1),![]() =(-1,-
=(-1,- ![]() ,0).
,0).
∴cos<![]() ,
,![]() >=
>=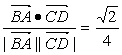 .
.
∴异面直线AB与CD所成角的大小为arccos![]() .
.
(3)解:设平面ACD的法向量为n=(x,y,z),
则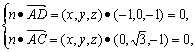
∴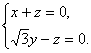 令y=1,得n=(-
令y=1,得n=(-![]() ,1,
,1,![]() ,)是平面ACD的一个法向量.
,)是平面ACD的一个法向量.
又![]() =(-
=(-![]() ,
,![]() ,0),
,0),
∴点E到平面ACD的距离h=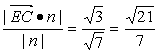


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源:高三数学教学与测试 题型:044
将一副三角板放在同一个平面上组成下图所示的四边形ACBD,△ABC中,∠C=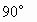 ,AC=BC,△ABD中,∠ABD=
,AC=BC,△ABD中,∠ABD=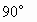 ,∠D=
,∠D=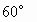 .设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).
.设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).
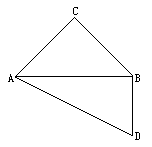
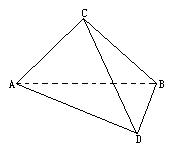
(1)求证:平面ACD⊥平面BCD;
(2)求直线AD和BC所成的角;
(3)求直线AD和平面BCD所成的角;
(4)求平面ACD和平面ABD所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源:广东省梅县东山中学2011-2012学年高二上学期期中考试数学理科试题 题型:013
如下图,AB是⊙O的直径,C是圆周上不同于A、B的任意一点,PA⊥平面ABC,则四面体P-ABC的四个面中,直角三角形的个数有

4个
3个
2个
1个
查看答案和解析>>
科目:高中数学 来源:英德中学2005~2006年高二数学选修(2-1)期末模拟考试题 题型:044
如下图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=![]() .F是线段PB上一点,
.F是线段PB上一点,![]() ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.

(Ⅰ)证明:PB⊥平面CEF;
(Ⅱ)求二面角B-CE-F的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
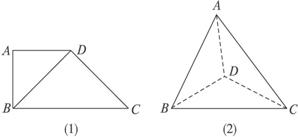
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com