
分析 (1)利用点到直线的距离求出半径,从而求圆的方程;
(2)利用圆心到直线的距离小于半径可求出实数a的取值范围
解答 解:(1)设圆心为M(m,0)(m∈Z).
由于圆与直线4x-3y+2=0相切,且半径为2,所以$\frac{|4m+2|}{5}$=2,
即|4m+2|=10.
因为m为整数,故m=2.
故所求的圆的方程是(x-2)2+y2=4.
(2)因为直线ax-y+5=0与圆总有公共点,
则圆心(2,0)到直线ax-y+5=0的距离不超过圆的半径,即$\frac{|2a-0+5|}{\sqrt{1+{a}^{2}}}$≤2,
解得a≤-$\frac{21}{20}$,
所以实数a的取值范围是(-∞,-$\frac{21}{20}$].
点评 本题主要考查了圆的标准方程,点到直线的距离公式,直线与圆的位置关系等知识的综合应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | -$\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “|x|>1”是“x>1”的必要不充分条件. | |
| B. | 若命题p:?x∈R,2x<3.则¬p:?x∈R,2x≥3. | |
| C. | 若p∧q为假命题,则p∨q也为假命题. | |
| D. | 命题“若x+y≠5,则x≠2或y≠3”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
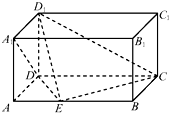 如图,已知在长方体ABCD-A1B1C1D1中,AD=A1A=$\frac{1}{2}$AB=2,点E是棱AB上一点,且$\frac{AE}{EB}$=λ.
如图,已知在长方体ABCD-A1B1C1D1中,AD=A1A=$\frac{1}{2}$AB=2,点E是棱AB上一点,且$\frac{AE}{EB}$=λ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 学生的性别与他的数学成绩 | B. | 人的工作环境与健康状况 | ||
| C. | 女儿的身高与父亲的身高 | D. | 正三角形的边长与面积 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | 5 | C. | $\frac{{5+2\sqrt{2}}}{4}$ | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com