
【题目】近期,西安公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:
![]()
根据以上数据,绘制了散点图.
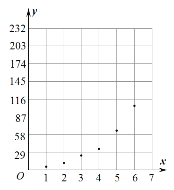
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数),哪一个适宜作为扫码支付的人次
均为大于零的常数),哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,建立![]() 与
与![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次;
的回归方程,并预测活动推出第8天使用扫码支付的人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下表:
![]()
西安公交六公司车队为缓解周边居民出行压力,以![]() 万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为
万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为![]() 万元.已知该线路公交车票价为
万元.已知该线路公交车票价为![]() 元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受
元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受![]() 折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有
折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有![]() 的概率享受
的概率享受![]() 折优惠,有
折优惠,有![]() 的概率享受
的概率享受![]() 折优惠,有
折优惠,有![]() 的概率享受
的概率享受![]() 折优惠.预计该车队每辆车每个月有
折优惠.预计该车队每辆车每个月有![]() 万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要
万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要![]() (
(![]() )年才能开始盈利,求
)年才能开始盈利,求![]() 的值.
的值.
参考数据:
|
|
|
|
|
|
|
|
|
|
其中其中![]() ,
,![]() ,
,
参考公式:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: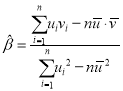 ,
,![]() .
.
【答案】(1)![]() (2)
(2)![]() ,3470(3)7
,3470(3)7
【解析】
(1)由散点图可知,更接近指数增长,所以![]() 适宜作为扫码支付的人次
适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型.
的回归方程类型.
(2)根据(1)的判断结果![]() 两边取对数得
两边取对数得![]() ,则
,则![]() 两者线性相关,根据已知条件求出
两者线性相关,根据已知条件求出![]() 得回归方程,进而得到y关于x的回归方程,再令
得回归方程,进而得到y关于x的回归方程,再令![]() ,求预测值
,求预测值
(3)设一名乘客一次乘车的费用为![]() 元,根据题意
元,根据题意![]() 得可能取值为:1.4、1.6、1.8、2,求出分布列,进而求得期望,然后再建立不等式求解.
得可能取值为:1.4、1.6、1.8、2,求出分布列,进而求得期望,然后再建立不等式求解.
(1)根据散点图判断,在推广期内, ![]() (
(![]() 均为大于零的常数),适宜作为扫码支付的人次
均为大于零的常数),适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型.
的回归方程类型.
(2)根据(1)的判断结果![]() ,
,
两边取对数得![]() ,
,
其中![]() ,
,![]() ,
,![]() ,
,
 ,
,
![]() ,
,
所以![]() 。
。
所以![]() 。
。
当![]() 时,
时, ![]() 。
。
所以活动推出第8天使用扫码支付的人次3470人.
(3)设一名乘客一次乘车的费用为![]() 元,
元,
根据题意![]() 得可能取值为:1.4、1.6、1.8、2
得可能取值为:1.4、1.6、1.8、2
![]() ,
,
![]() ,
,
![]() 。
。
假设这批车需要![]() (
(![]() )年才能开始盈利,
)年才能开始盈利,
则![]() ,
,
解得![]() 。
。
所以需要7年才能开始盈利.。


科目:高中数学 来源: 题型:
【题目】有下列说法:①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适.②相关指数![]() 来刻画回归的效果,
来刻画回归的效果,![]() 值越大,说明模型的拟合效果越好.③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.其中正确命题的个数是( )
值越大,说明模型的拟合效果越好.③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.其中正确命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率统计表和频率分布直方图如下:
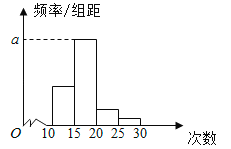
分组 | 频数 | 频率 |
| 15 | 0.30 |
| 29 |
|
|
|
|
| 2 |
|
合计 |
| 1 |
(1)求出表中![]() ,
,![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高三学生人数有500人,试估计该校高三学生参加社区服务的次数在区间![]() 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与抛物线
与抛物线![]() :
:![]() 的准线交于
的准线交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() :
:![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且曲线
两点,且曲线![]() 上存在两点
上存在两点![]() ,
,![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围及
的取值范围及![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() ,
,![]() .
.
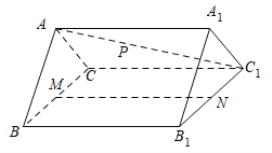
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的动点,若二面角
上的动点,若二面角![]() 的平面角的大小为
的平面角的大小为![]() ,试确定点
,试确定点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,侧面
中,侧面![]() 是边长为2的等边三角形且垂直于底面
是边长为2的等边三角形且垂直于底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
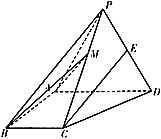
(1)求证:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且二面角
上,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与底面
与底面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系xOy中,设倾斜角为α的直线l:![]() (t为参数)与曲线C:
(t为参数)与曲线C:![]() (θ为参数)相交于不同的两点A,B.
(θ为参数)相交于不同的两点A,B.
(Ⅰ)若α=![]() ,求线段AB中点M的坐标;
,求线段AB中点M的坐标;
(Ⅱ)若|PA|·|PB|=|OP|![]() ,其中P(2,
,其中P(2,![]() ),求直线l的斜率.
),求直线l的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com