(1)求证：2n＋2·3n＋5n－4能被25整除；
(2)求证：1＋3＋32＋…＋33n－1能被26整除(n为大于1的偶数)．
(1)见解析 (2)见解析
【解析】
证明：(1)原式＝4(5＋1)n＋5n－4
＝4(C n05n＋C n15n－1＋Cn25n－2＋…＋Cnn)＋5n－4
＝4(C n05n＋C n15n－1＋…＋C nn-2·52＋C nn-1·51＋1)＋5n－4
＝4(C n05n＋C n15n－1＋…＋C nn-2·52)＋25n，
以上各项均为25的整数倍，故得证．
(2)因为1＋3＋32＋…＋33n－1＝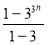
＝
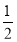(33n－1)
＝
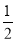(27n－1)＝
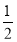[(26＋1)n－1]．
而(26＋1)n－1＝C n026n＋C n126n－1＋…＋C nn-126＋Cnn260－1
＝Cn026n＋Cn126n－1＋…＋Cnn-126
因为n为大于1的偶数，所以原式能被26整除．
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.5练习卷（解析版） 题型：填空题
某公司有5万元资金用于投资开发项目，如果成功，一年后可获利12%；如果失败，一年后将丧失全部资金的50%.下表是过去200例类似项目开发的实施结果：
投资成功 | 投资失败 |
192例 | 8例 |
则该公司一年后估计可获收益的数学期望是________元．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.3练习卷（解析版） 题型：填空题
一个袋中装有6个红球和4个白球(这10个球各不相同)，不放回地依次摸出2个球，在第一次摸出红球的条件下，第二次摸出红球的概率为________．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.1练习卷（解析版） 题型：解答题
设随机变量X的分布列为P(X＝i)＝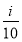
，(i＝1,2,3,4)．
(1)求P(X＜3)；
(2)求P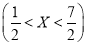
；
(3)求函数F(x)＝P(X＜x)．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标2.1练习卷（解析版） 题型：填空题
已知X的分布列为P(X＝k)＝
(k＝1,2，…，6)，其中c为常数，则P(X≤2)＝________.
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标1章练习卷（解析版） 题型：填空题
有甲、乙、丙三项任务，甲需2人承担，乙、丙各需1人承担，从10人中选派4人承担这项任务，不同的选法有________．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标1章练习卷（解析版） 题型：填空题
设集合A＝{1,2,3,4}，m，n∈A，则关于x，y的方程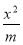
＋
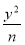＝1表示焦点在x轴上的椭圆的个数为________．
查看答案和解析>>
科目：高中数学 来源：2015届苏教版选修2-3高二数学双基达标1.2练习卷（解析版） 题型：解答题
用1,2,3,4,5五个数字组成无重复数字的五位数，其中恰有一个奇数夹在两个偶数之间的五位数个数是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
8的展开式中的常数项为________．