
【题目】已知函数 f(x)=ax+(1﹣a)lnx+![]() (a∈R)
(a∈R)
(Ⅰ)当a=0时,求 f(x)的极值;
(Ⅱ)当a<0时,求 f(x)的单调区间;
(Ⅲ)方程 f(x)=0的根的个数能否达到3,若能请求出此时a的范围,若不能,请说明理由.
【答案】
【解析】
试题(Ⅰ)代入a的值,求出定义域,求导,利用导数求出单调区间,即可求出极值;(Ⅱ)直接对f(x)求导,根据a的不同取值,讨论f(x)的单调区间;(Ⅲ)由第二问的结论,即函数的单调区间来讨论f(x)的零点个数.
试题解析:(Ⅰ)f(x)其定义域为(0,+∞).
当a=0时,f(x)=![]() ,f'(x)=
,f'(x)=![]() .
.
令f'(x)=0,解得x=1,
当0<x<1时,f'(x)<0;当x>1时,f'(x)>0.
所以f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞);
所以x=1时,f(x)有极小值为f(1)=1,无极大值
(Ⅱ) f'(x)=a﹣![]() (x>0)
(x>0)
令f'(x)=0,得x=1或x=﹣![]()
当﹣1<a<0时,1<﹣![]() ,令f'(x)<0,得0<x<1或x>﹣
,令f'(x)<0,得0<x<1或x>﹣![]() ,
,
令f'(x)>0,得1<x<﹣![]() ;
;
当a=﹣1时,f'(x)=﹣![]() .
.
当a<﹣1时,0<﹣![]() <1,令f'(x)<0,得0<x<﹣
<1,令f'(x)<0,得0<x<﹣![]() 或x>1,
或x>1,
令f'(x)>0,得﹣![]() <a<1;
<a<1;
综上所述:
当﹣1<a<0时,f(x)的单调递减区间是(0,1),(﹣![]() ),
),
单调递增区间是(1,﹣![]() );
);
当a=﹣1时,f(x)的单调递减区间是(0,+∞);
当a<﹣1时,f(x)的单调递减区间是(0,﹣![]() ),(1,+∞),单调递增区间是
),(1,+∞),单调递增区间是![]()
(Ⅲ)a≥0∴![]()
f'(x)=0(x>0)仅有1解,方程f(x)=0至多有两个不同的解.
(注:也可用fmin(x)=f(1)=a+1>0说明.)
由(Ⅱ)知﹣1<a<0时,极小值 f(1)a+1>0,方程f(x)=0至多在区间(﹣![]() )上有1个解.
)上有1个解.
a=﹣1时f(x)单调,方程f(x)=0至多有1个解.;
a<﹣1时,![]() ,方程
,方程
f(x)=0仅在区间内(0,﹣![]() )有1个解;
)有1个解;
故方程f(x)=0的根的个数不能达到3.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】某校从高一年级的一次月考成绩中随机抽取了 50名学生的成绩(满分100分,且抽取的学生成绩都在![]() 内),按成绩分为
内),按成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,得到如图所示的频率分布直方图.
五组,得到如图所示的频率分布直方图.
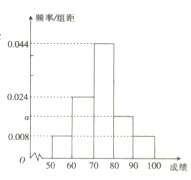
(1)用分层抽样的方法从月考成绩在![]() 内的学生中抽取6人,求分别抽取月考成绩在
内的学生中抽取6人,求分别抽取月考成绩在![]() 和
和![]() 内的学生多少人;
内的学生多少人;
(2)在(1)的前提下,从这6名学生中随机抽取2名学生进行调查,求月考成绩在![]() 内至少有1名学生被抽到的概率.
内至少有1名学生被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536—1611),明太祖九世孙,音乐家、数学家、天文历算家,在他多达百万字的著述中以《乐律全书》最为著名,在西方人眼中他是大百科全书式的学者王子。他对文艺的最大贡献是他创建了“十二平均律”,此理论被广泛应用在世界各国的键盘乐器上,包括钢琴,故朱载堉被誉为“钢琴理论的鼻祖”。“十二平均律”是指一个八度有13个音,相邻两个音之间的频率之比相等,且最后一个音频率是最初那个音频率的2倍,设第二个音的频率为![]() ,第八个音的频率为
,第八个音的频率为![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(请写出式子在写计算结果)有4个不同的小球,4个不同的盒子,现在要把球全部放入盒内:
(1)共有多少种方法?
(2)若每个盒子不空,共有多少种不同的方法?
(3)恰有一个盒子不放球,共有多少种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有12个球,其中5个红球,4个黑球,2个白球,1个绿球.从中随机取出1球,求:
(1)取出1球是红球或黑球的概率;
(2)取出1球是红球或黑球或白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个三棱锥的三个侧面中有两个是等腰直角三角形, 另一个是边长为 1 的正三角形.那么, 这个三棱锥的体积大小 ( ).
A. 有惟一确定的值 B. 有 2 个不同值
C. 有 3 个不同值 D. 有 3 个以上不同值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),当
为参数),当![]() 时,曲线
时,曲线![]() 上对应的点为
上对应的点为![]() .以原点
.以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设曲线![]() 与
与![]() 的公共点为
的公共点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com