
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),当
为参数),当![]() 时,曲线
时,曲线![]() 上对应的点为
上对应的点为![]() .以原点
.以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设曲线![]() 与
与![]() 的公共点为
的公共点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,且
的中点,且![]() .
.
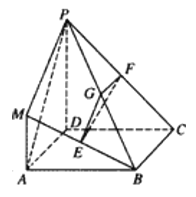
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之比.
的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有偶数个球,其中红球、黑球各占一半,甲、乙、丙是三个空盒.每次从袋中任取两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都放入盒中,则( )
A. 乙盒中红球与丙盒中黑球一样多
B. 乙盒中黑球不多于丙盒中黑球
C. 乙盒中红球不多于丙盒中红球
D. 乙盒中黑球与丙盒中红球一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)(i)利用(1)所求的回归方程,预测该市车流量为8万辆时![]() 的浓度;
的浓度;
(ii)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
参考公式:回归直线的方程是![]() ,其中
,其中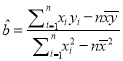 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:
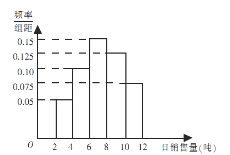
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用![]() 表示未来3天内日销售量不低于8吨的天数,求随机变量
表示未来3天内日销售量不低于8吨的天数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;
(2)设![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。
的图象交于B、C两点,B(2,m)且m<2,正方形ABCD的顶点A、D在坐标轴上。
⑴ 求![]() ,
, ![]() 的值;
的值;
⑵ 直接写出![]() 时,
时, ![]() 的取值范围。
的取值范围。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数![]() 在定义域内给定区间
在定义域内给定区间![]() 上存在
上存在![]() (
(![]() ),满足
),满足![]() ,则称函数
,则称函数![]() 是
是![]() 上的“平均值函数”,
上的“平均值函数”, ![]() 是它的一个均值点.如
是它的一个均值点.如![]() 是
是![]() 上的平均值函数,0就是他的均值点.
上的平均值函数,0就是他的均值点.
(1)判断函数![]() 在区间
在区间![]() 上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
(2)若函数![]() 是区间
是区间![]() 上的平均值函数,试确定实数
上的平均值函数,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com