
【题目】定义:如果函数![]() 在定义域内给定区间
在定义域内给定区间![]() 上存在
上存在![]() (
(![]() ),满足
),满足![]() ,则称函数
,则称函数![]() 是
是![]() 上的“平均值函数”,
上的“平均值函数”, ![]() 是它的一个均值点.如
是它的一个均值点.如![]() 是
是![]() 上的平均值函数,0就是他的均值点.
上的平均值函数,0就是他的均值点.
(1)判断函数![]() 在区间
在区间![]() 上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
(2)若函数![]() 是区间
是区间![]() 上的平均值函数,试确定实数
上的平均值函数,试确定实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),当
为参数),当![]() 时,曲线
时,曲线![]() 上对应的点为
上对应的点为![]() .以原点
.以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设曲线![]() 与
与![]() 的公共点为
的公共点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附: 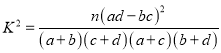 ,
, ![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是数学家伯努瓦·曼德尔布罗在![]() 世纪
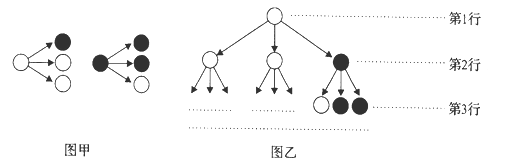
世纪![]() 年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图所示的分形规律可得如图乙所示的一个树形图:
年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图所示的分形规律可得如图乙所示的一个树形图:
若记图乙中第![]() 行白圈的个数为
行白圈的个数为![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心
的圆心![]() 在
在![]() 轴上,半径为1,直线
轴上,半径为1,直线![]() 被圆
被圆![]() 所截的弦长为
所截的弦长为![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 的下方.
的下方.
(1)求圆![]() 的方程;
的方程;
(2)设![]() ,若圆
,若圆![]() 是
是![]() 的内切圆,求
的内切圆,求![]() 的面积
的面积![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)甲、乙两袋中各装有大小相同的小球![]() 个,其中甲袋中红色、黑色、白色小球的个数分别为
个,其中甲袋中红色、黑色、白色小球的个数分别为![]() 、
、![]() 、
、![]() ,乙袋中红色、黑色、白色小球的个数均为
,乙袋中红色、黑色、白色小球的个数均为![]() ,某人用左右手分别从甲、乙两袋中取球.
,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com