
【题目】(I)若![]() ,
, ![]() 恒成立,求常数
恒成立,求常数![]() 的取值范.
的取值范.
(Ⅱ)已知非零常数![]() 、
、![]() 满足
满足![]() ,求不等式
,求不等式![]() 的解集;
的解集;
【答案】(1)![]() ,或
,或![]() ;(2),当
;(2),当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;当
;当![]() 时,原不等式的解集为
时,原不等式的解集为![]() .
.
【解析】试题分析:(1)问题转化为(![]() 1)(
1)( ![]() 2x+1)0,通过讨论
2x+1)0,通过讨论![]() 的范围求出不等式的解集,从而求出
的范围求出不等式的解集,从而求出![]() 的范围即可.
的范围即可.
(2)根据条件可得![]() ,进而
,进而![]() ,或
,或![]() ,分别讨论求解即可.
,分别讨论求解即可.
试题解析:
(1)由已知得,|x ![]() |x10,(x
|x10,(x ![]() )2(x1)2
)2(x1)2
∴(![]() 1)(
1)( ![]() 2x+1)0,
2x+1)0,
![]() =1时,(
=1时,( ![]() 1)(
1)( ![]() 2x+1)0恒成立
2x+1)0恒成立
![]() >1时,由(
>1时,由(![]() 1)(
1)( ![]() 2x+1)0得,
2x+1)0得, ![]() 2x1,从而
2x1,从而![]() 3
3
![]() <1时,由(
<1时,由(![]() 1)(
1)( ![]() 2x+1)0得,
2x+1)0得, ![]() 2x1,从而
2x1,从而![]() 1
1
综上所述,a的取值范围为(∞,1]∪[3,+∞)…(10分)
(2)![]() ,∴
,∴![]() ,
,
∴![]() ,或
,或![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,
,
∴![]() ,或
,或![]() ,∴
,∴![]() 或
或![]() ,
,
综上,当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]()


科目:高中数学 来源: 题型:
【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:
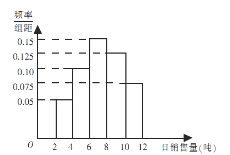
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用![]() 表示未来3天内日销售量不低于8吨的天数,求随机变量
表示未来3天内日销售量不低于8吨的天数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() )的图像关于坐标原点对称。
)的图像关于坐标原点对称。
(1)求![]() 的值,并求出函数
的值,并求出函数![]() 的零点;
的零点;
(2)若函数![]() 在
在![]() 内存在零点,求实数
内存在零点,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求满足条件的最小整数
上恒成立,求满足条件的最小整数![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)是奇函数,且满足f(x)=f(x+3),f(-2)=-3.若数列{an}中,a1=-1,且前n项和Sn满足![]() =2×
=2×![]() +1,则f(a5)+f(a6)=________.
+1,则f(a5)+f(a6)=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数![]() 在定义域内给定区间
在定义域内给定区间![]() 上存在
上存在![]() (
(![]() ),满足
),满足![]() ,则称函数
,则称函数![]() 是
是![]() 上的“平均值函数”,
上的“平均值函数”, ![]() 是它的一个均值点.如
是它的一个均值点.如![]() 是
是![]() 上的平均值函数,0就是他的均值点.
上的平均值函数,0就是他的均值点.
(1)判断函数![]() 在区间
在区间![]() 上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
(2)若函数![]() 是区间
是区间![]() 上的平均值函数,试确定实数
上的平均值函数,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
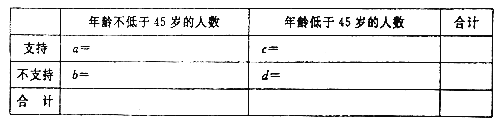
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:

(1)由以上统计数据填下面![]() 列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
(2)若对年龄在![]() 的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
(1)若对任意![]() ,且
,且![]() ,都有
,都有![]() ,则
,则![]() 为R上的减函数;
为R上的减函数;
(2)若![]() 为R上的偶函数,且在
为R上的偶函数,且在![]() 内是减函数,
内是减函数, ![]() (-2)=0,则
(-2)=0,则![]() >0解集为(-2,2);
>0解集为(-2,2);
(3)若![]() 为R上的奇函数,则
为R上的奇函数,则![]() 也是R上的奇函数;
也是R上的奇函数;
(4)t为常数,若对任意的![]() ,都有
,都有![]() 则
则![]() 关于
关于![]() 对称。
对称。
其中所有正确的结论序号为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过曲线C1:![]() -
-![]() =1(a>0,b>0)的左焦点F1作曲线C2:x2+y2=a2的切线,设切点为M,直线F1M交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若|MF1|=|MN|,则曲线C1的离心率为( )
=1(a>0,b>0)的左焦点F1作曲线C2:x2+y2=a2的切线,设切点为M,直线F1M交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若|MF1|=|MN|,则曲线C1的离心率为( )
A. ![]() B.
B. ![]() -1 C.
-1 C. ![]() +1 D.
+1 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com