练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知tan α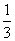＝－，cos β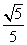＝，α，β∈(0，π)．

    (1)求tan(α＋β)的值；

    (2)求函数f(x)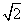＝sin(x－α)＋cos(x＋β)的最大值．


    解　(1)由cos β＝，β∈(0，π)，

    得sin β＝，tan β＝2，

    所以tan(α＋β)＝＝1.

    (2)因为tan α＝－，α∈(0，π)，

    所以sin α＝，cos α＝－，

    f(x)＝(sin xcos α－cos xsin α)＋cos xcos β－sin xsin β

    ＝－sin x－cos x＋cos x－sin x

    ＝－sin x，

    又－1≤sin x≤1，所以f(x)的最大值为.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某商店预备在一个月内分批购买每张价值为20元的书桌共36台，每批都购入x台(x是正整数)，且每批均需付运费4元，储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比，若每批购入4台，则该月需用去运费和保管费共52元，现在全月只有48元资金可以用于支付运费和保管费．

    (1)求该月需用去的运费和保管费的总费用f(x)；

    (2)能否恰当地安排每批进货的数量，使资金够用？写出你的结论，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如右图所示，函数y＝2cos(ωx＋θ)(x∈R，ω>0,0≤θ≤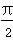)的图象与y轴交于点(0，)，且该函数的最小正周期为π.

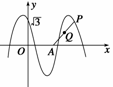
    (1)求θ和ω的值；

    (2)已知点A(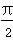，0)，点P是该函数图象上一点，点Q(x0，y0)是PA的中点，当y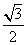0＝，x0∈[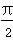，π]时，求x0的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若0<x<，则2x与πsin x的大小关系是(　　)

    A．2x>πsin x         B．2x<πsin x

    C．2x＝πsin x        D．与x的取值有关

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设△ABC的三个内角为A，B，C，向量m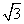＝(sin A，sin B)，n＝(cos B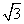，cos A)，若m·n＝1＋cos(A＋B)，则C的值为(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝的图象的一条对称轴方程是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＝sin 17°cos 45°＋cos 17°sin 45°，b＝2cos213°－1，c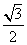＝，则有(　　)

    A．c<a<b        B．b<c<a

    C．a<b<c        D．b<a<c

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝sin x－cos x(x∈[－π，0])的单调递增区间是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设变量x，y满足约束条件则目标函数z＝|x＋3y|的最大值为(　　)

    A．4                     B．6

    C．8                     D．10

    查看答案和解析>>

    同步练习册答案