
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 由题意可得函数y=$\frac{1}{x-1}$的图象(红色部分)与函数y=2sinπx(-3≤x≤5)的图象所有交点关于点(1,0)对称,它们共有8个交点,构成4对,且每一对关于点(1,0)对称,由此求得所有交点的横坐标之和.
解答 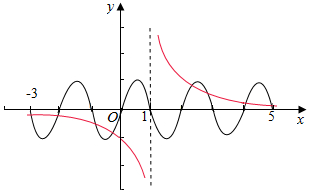 解:函数y=$\frac{1}{x-1}$的图象关于点(1,0)对称,函数y=2sinπx(-3≤x≤5)的图象也关于点(1,0)对称,如图所示:
解:函数y=$\frac{1}{x-1}$的图象关于点(1,0)对称,函数y=2sinπx(-3≤x≤5)的图象也关于点(1,0)对称,如图所示:
故函数y=$\frac{1}{x-1}$的图象(红色部分)与函数y=2sinπx(-3≤x≤5)的图象所有交点关于点(1,0)对称,
它们共有8个交点,构成4对,且每一对关于点(1,0)对称,
故他们的横坐标之和为4×2=8,
故选:D.
点评 本题主要考查函数的图象特征,判断他们的交点关于点(1,0)对称,是解题的关键,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
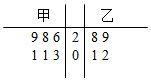 为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6,6 | B. | 5,6 | C. | 5,5 | D. | 6,5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com