
 Ϊ�Ƚϼס�������ij��14ʱ������״�������ѡȡ�����е�5�죬����5����14ʱ���������ݣ���λ���棩�Ƴ���ͼ��ʾ�ľ�Ҷͼ���������½��ۣ�
Ϊ�Ƚϼס�������ij��14ʱ������״�������ѡȡ�����е�5�죬����5����14ʱ���������ݣ���λ���棩�Ƴ���ͼ��ʾ�ľ�Ҷͼ���������½��ۣ����� ����֪�ľ�Ҷͼ�������������ס��Ҽף�������ij��14ʱ�����³�ȡ�������¶ȣ���������������ݵ�ƽ������������ɵô𰸣�
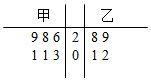
��� �⣺�ɾ�Ҷͼ�е����ݣ����ǿɵüס��Ҽף�������ij��14ʱ�����³�ȡ�������¶ȷֱ�Ϊ��
�ף�26��28��29��31��31
�ң�28��29��30��31��32��
�ɵã��ظ���14ʱ��ƽ�����£�$\frac{1}{5}$��26+28+29+31+31��=29��
�ҵظ���14ʱ��ƽ�����£�$\frac{1}{5}$��28+29+30+31+32��=30��
�ʼظ���14ʱ��ƽ�����µ����ҵظ���14ʱ��ƽ�����£�
�ظ���14ʱ�¶ȵķ���Ϊ��S��2=$\frac{1}{5}$[��26-29��2+��28-29��2+��29-29��2+��31-29��2+��31-29��2]=3.6
�ҵظ���14ʱ�¶ȵķ���Ϊ��S��2=$\frac{1}{5}$[��28-30��2+��29-30��2+��30-30��2+��31-30��2+��32-30��2]=2��
��S��2��S��2��
���Լظ���14ʱ�����µı�������ҵظ���14ʱ�����±��
�ʴ�Ϊ���٢ܣ�
���� ���⿼�����ݵ���ɢ�̶��뾥Ҷͼ��״�Ĺ�ϵ������ѧ���ļ������������ڻ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60��50��40 | B�� | 50��60��40 | C�� | 40��50��60 | D�� | 60��40��50 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{\sqrt{2}}{2}$] | B�� | [$\frac{\sqrt{2}}{2}$��$\frac{\sqrt{5}}{3}$] | C�� | [$\frac{2}{3}$��$\frac{\sqrt{5}}{3}$] | D�� | [$\frac{\sqrt{5}}{3}$��1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com