
| A. | (0,$\frac{\sqrt{2}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{5}}{3}$] | C. | [$\frac{2}{3}$,$\frac{\sqrt{5}}{3}$] | D. | [$\frac{\sqrt{5}}{3}$,1) |
分析 设F1(-c,0),F2(c,0),运用椭圆的定义和勾股定理,求得e2=$\frac{{λ}^{2}+1}{(λ+1)^{2}}$,令m=λ+1,可得λ=m-1,即有$\frac{{λ}^{2}+1}{(λ+1)^{2}}$=$\frac{{m}^{2}-2m+2}{{m}^{2}}$=2($\frac{1}{m}$-$\frac{1}{2}$)2+$\frac{1}{2}$,运用二次函数的最值的求法,解不等式可得所求范围.
解答 解:设F1(-c,0),F2(c,0),由椭圆的定义可得,|PF1|+|PF2|=2a,
可设|PF2|=t,可得|PF1|=λt,
即有(λ+1)t=2a①
由∠F1PF2=$\frac{π}{2}$,可得|PF1|2+|PF2|2=4c2,
即为(λ2+1)t2=4c2,②
由②÷①2,可得e2=$\frac{{λ}^{2}+1}{(λ+1)^{2}}$,
令m=λ+1,可得λ=m-1,
即有$\frac{{λ}^{2}+1}{(λ+1)^{2}}$=$\frac{{m}^{2}-2m+2}{{m}^{2}}$=2($\frac{1}{m}$-$\frac{1}{2}$)2+$\frac{1}{2}$,
由$\frac{1}{2}$≤λ≤2,可得$\frac{3}{2}$≤m≤3,即$\frac{1}{3}$≤$\frac{1}{m}$≤$\frac{2}{3}$,
则m=2时,取得最小值$\frac{1}{2}$;m=$\frac{3}{2}$或3时,取得最大值$\frac{5}{9}$.
即有$\frac{1}{2}$≤e2≤$\frac{5}{9}$,解得$\frac{\sqrt{2}}{2}$≤e≤$\frac{\sqrt{5}}{3}$.
故选:B.
点评 本题考查椭圆的定义、方程和性质,主要考查离心率的范围,同时考查不等式的解法,属于中档题.


科目:高中数学 来源: 题型:填空题
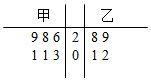 为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±3x | B. | y=±$\sqrt{3}$x | C. | y=±x | D. | y=±$\frac{\sqrt{3}}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com