练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

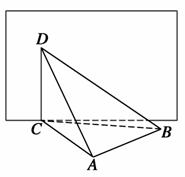
    为扑灭某着火点，现场安排了两支水枪，如图，D是着火点，A、B分别是水枪位置，已知AB＝15 m，在A处看到着火点的仰角为60°，∠ABC＝30°，∠BAC＝105°，求两支水枪的喷射距离至少是多少？


    解　在△ABC中，可知∠ACB＝45°，

    由正弦定理，得＝，

    解得AC＝15 m.

    又∵∠CAD＝60°，∴AD＝30，CD＝15，

    综上可知，两支水枪的喷射距离至少分别为30 m，15 m.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知A、B、C是三角形的内角，sinA，－cosA是方程x2－x＋2a＝0的两根．

    (1)求角A；

    (2)若＝－3，求tanB.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将函数f(x)＝2sin(ωx＋φ)(ω>0,0<φ<π)的图象向右平移个单位长度后得到g(x)的图象，已知g(x)的部分图象如图所示，该图象与y轴相交于点F(0,1)，与x轴相交于点P，Q，点M为最高点，且△MPQ的面积为.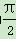

    (1)求函数g(x)的解析式；

    (2)在△ABC中，a，b，c分别是角A，B，C的对边，g(A)＝1，且a＝，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，三边长a，b，c满足a3＋b3＝c3，那么△ABC的形状为(　　)

    A．锐角三角形                           B．钝角三角形

    C．直角三角形                           D．以上均有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    线段AB外有一点C，∠ABC＝60°，AB＝200 km，汽车以80 km/h的速度由A向B行驶，同时摩托车以50 km/h的速度由B向C行驶，则运动开始多少h后，两车的距离最小(　　)

    A.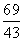                                   B．1

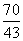    C.                                   D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在等腰直角△OPQ中，∠POQ＝90°，OP＝2，点M在线段PQ上．

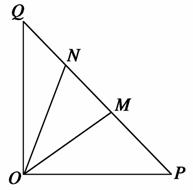
    (1)若OM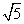＝，求PM的长；

    (2)若点N在线段MQ上，且∠MON＝30°，问：当∠POM取何值时，△OMN的面积最小？并求出面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若，则四边形ABCD的形状是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中，四边形ABCD的边AB∥DC，AD∥BC.已知点A(－2,0)，B(6,8)，C(8,6)，则D点的坐标为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若三角形的一个内角等于另外两个内角之差，则这个三角形是（　　）

    　 A． 锐角三角形 B． 直角三角形 C． 钝角三角形 D． 不能确定

     

    查看答案和解析>>

    同步练习册答案