
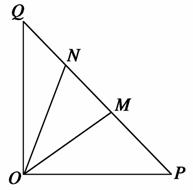
如图,在等腰直角△OPQ中,∠POQ=90°,OP=2 ,点M在线段PQ上.
,点M在线段PQ上.
(1)若OM=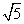 ,求PM的长;
,求PM的长;
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
科目:高中数学 来源: 题型:
轮船A和轮船B在中午12时离开海港C,两艘轮船航行方向的夹角为120°,轮船A的航行速度是25海里/小时,轮船B的航行速度是15海里/小时,下午2时两船之间的距离是( )
A.35海里 B.35 海里
海里
C.35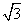 海里 D.70海里
海里 D.70海里
查看答案和解析>>
科目:高中数学 来源: 题型:
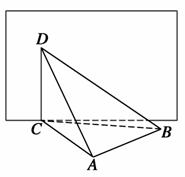
为扑灭某着火点,现场安排了两支水枪,如图,D是着火点,A、B分别是水枪位置,已知AB=15 m,在A处看到着火点的仰角为60°,∠ABC=30°,∠BAC=105°,求两支水枪的喷射距离至少是多少?
m,在A处看到着火点的仰角为60°,∠ABC=30°,∠BAC=105°,求两支水枪的喷射距离至少是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
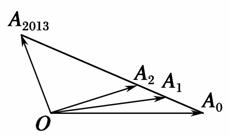
如图,O为线段A0A2 013外一点,若A0,A1,A2,A3,…,A2 013中任意相邻两点的距离相等,OA0=a,OA2 013=b,用a,b表示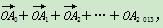 其结果为( )
其结果为( )
A.1 006(a+b)
B.1 007(a+b)
C.2 012(a+b)
D.2 014(a+b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com