
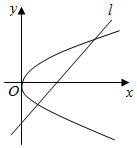
 如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).
如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).分析 (1)求出抛物线的焦点坐标,然后求解抛物线方程.
(2):①设点P(x1,y1),Q(x2,y2),通过抛物线方程,求解kPQ,通过P,Q关于直线l对称,点的kPQ=-1,推出$\frac{{y}_{1}+{y}_{2}}{2}=-p$,PQ的中点在直线l上,推出$\frac{{x}_{1}+{x}_{2}}{2}$=2-p,即可证明线段PQ的中点坐标为(2-p,-p);
②利用线段PQ中点坐标(2-p,-p).推出$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=-2p}\\{{y}_{1}{y}_{2}=4{p}^{2}-4p}\end{array}\right.$,得到关于y2+2py+4p2-4p=0,有两个不相等的实数根,列出不等式即可求出p的范围.
解答 解:(1)∵l:x-y-2=0,∴l与x轴的交点坐标(2,0),
即抛物线的焦点坐标(2,0).
∴$\frac{p}{2}=2$,
∴抛物线C:y2=8x.
(2)证明:①设点P(x1,y1),Q(x2,y2),则:$\left\{\begin{array}{l}{{{y}_{1}}^{2}=2p{x}_{1}}\\{{{y}_{2}}^{2}=2p{x}_{2}}\end{array}\right.$,
即:$\left\{\begin{array}{l}{\frac{{{y}_{1}}^{2}}{2p}={x}_{1}}\\{\frac{{{y}_{2}}^{2}}{2p}={x}_{2}}\end{array}\right.$,kPQ=$\frac{{y}_{1}{-y}_{2}}{\frac{{{y}_{1}}^{2}}{2p}-\frac{{{y}_{2}}^{2}}{2p}}$=$\frac{2p}{{y}_{1}+{y}_{2}}$,
又∵P,Q关于直线l对称,∴kPQ=-1,即y1+y2=-2p,∴$\frac{{y}_{1}+{y}_{2}}{2}=-p$,
又PQ的中点在直线l上,∴$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{{y}_{1}+{y}_{2}}{2}+2$=2-p,
∴线段PQ的中点坐标为(2-p,-p);
②因为Q中点坐标(2-p,-p).
∴$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=-2p}\\{{x}_{1}+{x}_{2}=\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}}{2p}=4-2p}\end{array}\right.$,即$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=-2p}\\{{{y}_{1}}^{2}+{{y}_{2}}^{2}=8p-4{p}^{2}}\end{array}\right.$
∴$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=-2p}\\{{y}_{1}{y}_{2}=4{p}^{2}-4p}\end{array}\right.$,即关于y2+2py+4p2-4p=0,有两个不相等的实数根,
∴△>0,(2p)2-4(4p2-4p)>0,
∴p∈$(0,\frac{4}{3})$.
点评 本题考查抛物线方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及计算能力.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
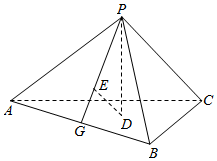 如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com