练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设为椭圆：的下顶点，椭圆长半轴的长等于椭圆的短轴长，且椭圆经过点.

    （1）求椭圆的方程；

    （2）过点的直线与直线交于点，与椭圆交于，点关于原点的对称点为，直线交直线交于点，求的最小值.

    【答案】（1）；（2）的最小值为4

    【解析】

    （1）依题意，则，代入求解即可得到结果；

    （2）由题意可知直线的斜率存在且不为0，设直线的方程为，联立，得到，联立，得到，，结合点A可得直线的方程为，当时求得，所以，不妨设，再利用基本不等式即可求出最小值.

    （1）依题意，则，代入，解得，所以；

    （2）由题意可知直线的斜率存在且不为0，设直线的方程为，

    ，，所以，

    ，消去得，解得，，

    所以，则，

    所以直线的斜率，

    直线的方程为，当时，，所以，则，不妨设，，当且仅当即时等号成立，所以的最小值为4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）当a=0时，求函数f（x）在（1，f（1））处的切线方程；

    （2）令求函数的极值.

    （3）若，正实数满足，

    证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    在平面直角坐标系xOy中，曲线C的参数方程为（a为参数），在以原点为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为.

    （1）求C的普通方程和l的倾斜角；

    （2）设点，l和C交于A，B两点，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动，有N个人参加，现将所有参加者按年龄情况分为等七组，其频率分布直方图如图所示，已知这组的参加者是6人.

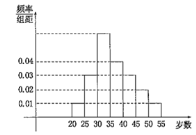
    （1）根据此频率分布直方图求N；

    （2）组织者从这组的参加者（其中共有4名女教师，其余全为男教师）中随机选取3名担任后勤保障工作，其中女教师的人数为X，求X的分布列、均值及方差.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:

    消费次第

    第次

    第次

    第次

    第次

    次

    收费比率

    该公司注册的会员中没有消费超过次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:

    消费次数

    次

    次

    次

    次

    次

    人数

    假设汽车美容一次,公司成本为元,根据所给数据,解答下列问题:

    （1）某会员仅消费两次,求这两次消费中,公司获得的平均利润;

    （2）以事件发生的频率作为相应事件发生的概率,设该公司为一位会员服务的平均利润为元,求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数在上为增函数，求的取值范围；

    （2）若函数有两个不同的极值点，记作，，且，证明：（为自然对数）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图（1）所示，在中，是边上的高，且，，是的中点．现沿进行翻折，使得平面平面，得到的图形如图（2）所示．

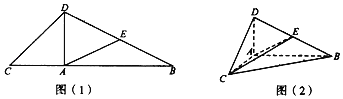
    （1）求证：；

    （2）求直线与平面所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直四棱柱中，底面是矩形，与交于点，.

    （1）证明：平面；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，是椭圆：上的两点，线段的中点在直线上.

    （1）当直线的斜率存在时，求实数的取值范围；

    （2）设是椭圆的左焦点，若椭圆上存在一点，使，求的值.

    查看答案和解析>>

    同步练习册答案