练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设二次函数f(x)＝ax2＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m＜n)．

    (1)若m＝－1，n＝2，求不等式F(x)＞0的解集；

    (2)若a＞0，且0＜x＜m＜n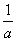＜，比较f(x)与m的大小．


    解：(1)由题意知，F(x)＝f(x)－x＝a(x－m)(x－n)，

    当m＝－1，n＝2时，不等式F(x)＞0，

    即a(x＋1)(x－2)＞0.

    那么当a＞0时，不等式F(x)＞0的解集为{x|x＜－1，或x＞2}；

    当a＜0时，不等式F(x)＞0 的解集为{x|－1＜x＜2}．

    (2)f(x)－m＝a(x－m)(x－n)＋x－m＝

    (x－m)(ax－an＋1)，

    ∵a＞0，且0＜x＜m＜n＜，∴x－m＜0，

    1－an＋ax＞0.

    ∴f(x)－m＜0，即f(x)＜m.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设全集是实数集，

    ,,则（     ）

    A．       B．   C．     D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    执行如图2的程序框图，如果输入的的值是，那么输出的的值是（     ）

    A.       B.                    C.                     D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某企业去年年底给全部的800名员工共发放2 000万元年终奖，该企业计划从今年起，10年内每年发放的年终奖都比上一年增加60万元，企业员工每年净增a人．

    (1)若a＝10，在计划时间内，该企业的人均年终奖是否会超过3万元？

    (2)为使人均年终奖年年有增长，该企业每年员工的净增量不能超过多少人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若不等式x2＋ax－2>0在区间[1,5]上有解，则a的取值范围是(　　)

    A.                         B.

    C．(1，＋∞)                          D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)是奇函数，g(x)是偶函数，且f(－1)＋g(1)＝2，f(1)＋g(－1)＝4，则g(1)等于(　　)

    A．4                                 B．3

    C．2                                 D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝|x－3|－|x＋1|的(　　)

    A．最小值是0，最大值是4            B．最小值是－4，最大值是0

    C．最小值是－4，最大值是4          D．没有最大值也没有最小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)的定义域A＝{x|0≤x≤2}，值域B＝{y|1≤y≤2}，下列选项中，能表示f(x)的图象的只可能是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的图象大致是（ ）

     

    查看答案和解析>>

    同步练习册答案