
已知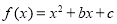 为偶函数,曲线
为偶函数,曲线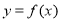 过点
过点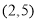 ,
, 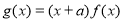 .
.
(1)若曲线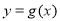 有斜率为0的切线,求实数
有斜率为0的切线,求实数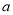 的取值范围;
的取值范围;
(2)若当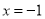 时函数
时函数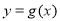 取得极值,确定
取得极值,确定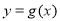 的单调区间.
的单调区间.
(1) 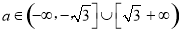 ;(2)
;(2)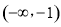 和
和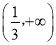 为
为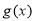 的单调递增区间,
的单调递增区间,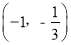 为
为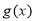 的单调递增区间.
的单调递增区间.
【解析】
试题分析:(1)先根据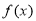 为偶函数,得到
为偶函数,得到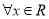 ,恒有
,恒有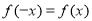 ,进而计算出
,进而计算出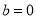 (也可根据二次函数的图像与性质得到对称轴
(也可根据二次函数的图像与性质得到对称轴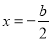 ,该对称轴为
,该对称轴为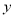 轴,进而得出
轴,进而得出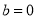 ),然后将点
),然后将点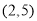 代入求出
代入求出 ,进而写出
,进而写出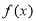 的表达式,此时
的表达式,此时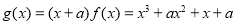 ,根据条件
,根据条件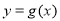 有斜率为0的切线即
有斜率为0的切线即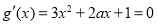 有实数解,根据二次方程有解的条件可得
有实数解,根据二次方程有解的条件可得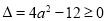 ,求解出
,求解出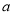 的取值范围即可;(2)先根据
的取值范围即可;(2)先根据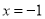 时函数
时函数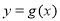 取得极值,得到
取得极值,得到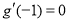 ,进而求出
,进而求出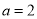 ,然后确定导函数
,然后确定导函数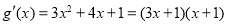 ,由导数
,由导数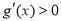 可求出函数的单调增区间,由
可求出函数的单调增区间,由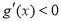 可求出函数的单调减区间.
可求出函数的单调减区间.
(1) 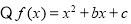 为偶函数,故对
为偶函数,故对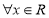 ,总有
,总有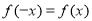 ,易得
,易得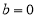
又曲线 过点
过点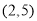 ,得
,得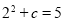 ,得
,得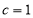 ,
,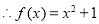 3分
3分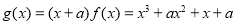
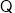 曲线
曲线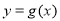 有斜率为0的切线,故
有斜率为0的切线,故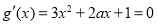 有实数解
有实数解
此时有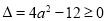 ,解得
,解得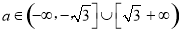 5分
5分
(2)因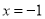 时函数
时函数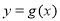 取得极值,故有
取得极值,故有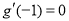 ,解得
,解得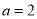
又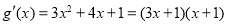 ,令
,令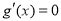 ,得
,得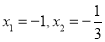 .
.
当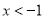 时,
时,
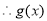 在
在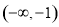 上为增函数
上为增函数
当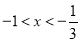 时,
时,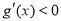 ,
,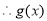 在
在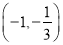 上为减函数
上为减函数
当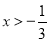 时,
时,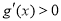 ,
,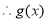 在
在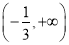 上为增函数
上为增函数
从而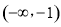 和
和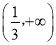 为
为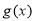 的单调递增区间,
的单调递增区间,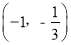 为
为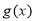 的单调递增区间 10分.
的单调递增区间 10分.
考点:1.函数的奇偶性;2.导数的几何意义;3.函数的极值与导数;4.函数的单调性与导数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
椭圆
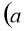 >
>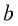 >
>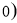 与直线
与直线 交于
交于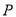 、
、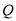 两点,且
两点,且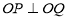 ,其中
,其中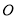 为坐标原点.
为坐标原点.
(1)求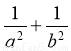 的值;
的值;
(2)若椭圆的离心率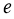 满足
满足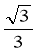 ≤
≤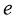 ≤
≤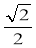 ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
某大学数学系共有本科生1 000人,其中一、二、三、四年级的人数比为4∶3∶2∶1,要用分层抽样的方法从所有本科生中抽取一个容量为200的样本,则应抽取三年级的学生人数为( ).
A.80 B.40 C.60 D.20
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期中考试文科数学试卷(解析版) 题型:填空题
在平面上,到直线的距离等于定长的点的轨迹是两条平行直线.类比在空间中:
(1)到定直线的距离等于定长的点的轨迹是 ;
(2)到已知平面相等的点的轨迹是 .
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.

(1)学校规定:成绩不低于75分的为优秀.请画出下面的 列联表.
列联表.
| 甲班 | 乙班 | 合计 |
优秀 |
|
|
|
不优秀 |
|
|
|
合计 |
|
|
|
(2)判断有多大把握认为“成绩优秀与教学方式有关”.
下面临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com