
| A. | x-3y=0 | B. | x+3y=0 | C. | 3x-y=0 | D. | 3x+y=0 |
分析 利用辅助角公式将函数进行化简,求出函数的对称轴即可得到结论.
解答 解:f(x)=asinx+bcosx=$\sqrt{{a}^{2}+{b}^{2}}$($\frac{a}{\sqrt{{a}^{2}+{b}^{2}}}$sinx+$\frac{b}{\sqrt{{a}^{2}+{b}^{2}}}$cosx),
令sinα=$\frac{a}{\sqrt{{a}^{2}+{b}^{2}}}$,则cosα=$\frac{b}{\sqrt{{a}^{2}+{b}^{2}}}$,即tanα=$\frac{a}{b}$,
则f(x)=$\sqrt{{a}^{2}+{b}^{2}}$cos(x-α),
由x-α=kπ,得x=α+kπ,k∈Z,
即函数的对称轴为x=α+kπ,k∈Z,
∵x=x0是函数f(x)的一条对称轴,
∴x0=α+kπ,则tanx0=tanα=$\frac{a}{b}$=3,即a=3b,
即a-3b=0,
则点(a,b)所在的直线为x-3y=0,
故选:A
点评 本题主要考查三角函数的化简,以及三角函数的图象和性质,利用辅助角公式将函数进行化简是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $f({-\frac{3}{2}})>f({{a^2}+2a+\frac{5}{2}})$ | B. | $f({-\frac{3}{2}})<f({{a^2}+2a+\frac{5}{2}})$ | C. | $f({-\frac{3}{2}})≥f({{a^2}+2a+\frac{5}{2}})$ | D. | $f({-\frac{3}{2}})≤f({{a^2}+2a+\frac{5}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
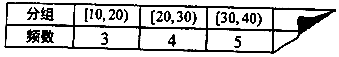
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 看营养说明 | 不看营养说明 | 合计 | |
| 男大学生 | 26 | 6 | 32 |
| 女大学生 | 14 | 18 | 32 |
| 合计 | 40 | 24 | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 1 | 2 | 3 | 4 | …第一行 |
| 2 | 3 | 4 | 5 | …第二行 |
| 3 | 4 | 5 | 6 | …第三行 |
| 4 | 5 | 6 | 7 | …第四行 |
| 第一列 | 第二列 | 第三列 | 第四列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com