
分析 (1)求出圆心C(a,2),半径r=2,圆心到直线l:x-y+3=0的距离,通过勾股定理求解即可.
(2)判断点与圆的位置关系,通过①当切线方程的斜率存在时,设方程为y-5=k(x-3),由圆心到切线的距离d=r求解即可;②当过(3,5)斜率不存在,判断直线x=3与圆是否相切,推出结果.
解答 解:(1)依题意可得圆心C(a,2),半径r=2,
则圆心到直线l:x-y+3=0的距离$d=\frac{{|{a-2+3}|}}{{\sqrt{{1^2}+{{(-1)}^2}}}}=\frac{{|{a+1}|}}{{\sqrt{2}}}$,
由勾股定理可知${d^2}+{(\frac{{2\sqrt{2}}}{2})^2}={r^2}$,代入化简得|a+1|=2,
解得a=1或a=-3,又a>0,
所以a=1;…(5分)
(2)由(1)知圆C:(x-1)2+(y-2)2=4,又(3,5)在圆外,
∴①当切线方程的斜率存在时,设方程为y-5=k(x-3),由圆心到切线的距离d=r=2可解得$k=\frac{5}{12}$,
∴切线方程为5x-12y+45=0…(9分),
②当过(3,5)斜率不存在,易知直线x=3与圆相切,
综合①②可知切线方程为5x-12y+45=0或x=3…(10分)
点评 本题考查直线与圆的位置关系的应用,点到直线的距离公式的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
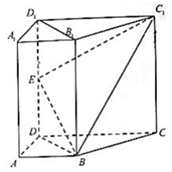 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-3y=0 | B. | x+3y=0 | C. | 3x-y=0 | D. | 3x+y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
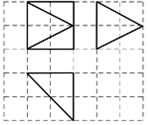 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
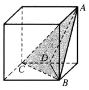 如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )
如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )| A. | 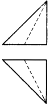 | B. | 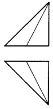 | C. | 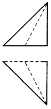 | D. | 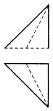 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{2}$,$\frac{3π}{4}$] | B. | [$\frac{π}{4}$,$\frac{3π}{4}$] | C. | [$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com