练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知某条曲线的参数方程是$\left\{\begin{array}{l}x=2（t+\frac{1}{t}）\\ y=2（t-\frac{1}{t}）\end{array}$（t是参数），则该曲线是（　　）
    A．直线B．圆C．椭圆D．双曲线

    分析 根据题意，将曲线的参数方程化为普通方程，结合双曲线的方程分析可得答案．

    解答 解：根据题意，某条曲线的参数方程是$\left\{\begin{array}{l}x=2（t+\frac{1}{t}）\\ y=2（t-\frac{1}{t}）\end{array}$，
    其普通方程为：x2-y2=16，
    则该曲线是双曲线；
    故选：D．

    点评 本题考查参数方程的应用，关键是将曲线的参数方程转化为普通方程．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．已知复数z满足：z（2-i）=3+i（其中i为虚数单位），则z的模等于$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=x-1-alnx（a＜0）．
    （1）讨论f（x）的单调性；
    （2）若对任意x1，x2∈（0，1]，且x1≠x2，都有$|f（{x_1}）-f（{x_2}）|＜4|\frac{1}{x_1}-\frac{1}{x_2}|$，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．调查者通过询问64名男女大学生在购买食品时是否看营养说明，得到的数据如表所示：
    看营养说明不看营养说明合计
    男大学生26632
    女大学生141832
    合计402464
    问大学生的性别与是否看营养说明之间有没有关系？
    附：参考公式与数据：χ2=$\frac{{n{{（n}_{11}n}_{22}{{-n}_{12}n}_{21}）}^{2}}{{n}_{1}{+n}_{2}{{+n}_{+1}n}_{+2}}$．当χ2＞3.841时，有95%的把握说事件A与B有关；当χ2＞6.635时，有99%的把握说事件A与B有关；当χ2≤3.841时，有95%的把握说事件A与B是无关的．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知圆C：x2+y2-2x+a=0，设AB为圆C的一条直径，$\overrightarrow{OA}•\overrightarrow{OB}$=-6（O为坐标原点），则a的值为-6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知直线l：x-y+3=0被圆C：（x-a）2+（y-2）2=4（a＞0）截得的弦长为$2\sqrt{2}$，求
    （1）a的值；
    （2）求过点（3，5）并与圆C相切的切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知曲线C的极坐标方程为ρ-4cosθ+3ρsin2θ=0，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l过点M（1，0），倾斜角为$\frac{π}{6}$．
    （Ⅰ）求曲线C的直角坐标方程与直线l的参数方程；
    （Ⅱ）若曲线C经过伸缩变换$\left\{\begin{array}{l}{x′=x}\\{y′=2y}\end{array}\right.$后得到曲线C′，且直线l与曲线C′交于A，B两点，求|MA|+|MB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在极坐标系中，圆ρ=-2cosθ的圆心C到直线2ρcosθ+ρsinθ-2=0的距离等于$\frac{4\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

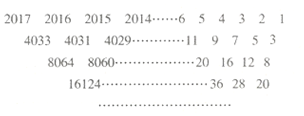    3．“杨辉三角”又称“贾宪三角”，是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算，而杨辉在公元1261年所著的《详解九章算法》一书中，辑录了贾宪三角形数表，并称之为“开方作法本源”图．下列数表的构造思路就源于“杨辉三角”．该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数是（　　）
    A．2017×22016B．2018×22015C．2017×22015D．2018×22016

    查看答案和解析>>

    同步练习册答案