
���� ��������C�ļ����귽�̻�Ϊ��2-4��cos��+3��2sin2��=0���ɴ����������C��ֱ�����귽�̣���ֱ��l����M��1��0������б��Ϊ$\frac{��}{6}$�������ֱ��l�IJ������̣�
����������C���������任$\left\{\begin{array}{l}{x��=x}\\{y��=2y}\end{array}\right.$��õ�����C�䣬�������C��Ϊ����x-2��2+y2=4����ֱ��l�IJ������̴�������C�䣬�ã�${t}^{2}-\sqrt{3}t-3=0$����A��B��Ӧ�IJ����ֱ�Ϊt1��t2����t1+t2=$\sqrt{3}$��t1t2=-3���ɴ������|MA|+|MB|��
��� �⣺��������C�ļ����귽��Ϊ��-4cos��+3��sin2��=0�����2-4��cos��+3��2sin2��=0��
������C��ֱ�����귽��Ϊx2+y2-4x+3y2=0���������ã�x-2��2+4y2=4��
��ֱ��l����M��1��0������б��Ϊ$\frac{��}{6}$��
��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{y=1+tcos\frac{��}{6}}\\{y=tsin\frac{��}{6}}\end{array}\right.$����$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$����t�Dz�������
��������C���������任$\left\{\begin{array}{l}{x��=x}\\{y��=2y}\end{array}\right.$��õ�����C�䣬
������C������x-2��2+y2=4��
��ֱ��l�IJ�������$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$����t�Dz�������������C�䣺��x-2��2+y2=4���ã�
${t}^{2}-\sqrt{3}t-3=0$��
��A��B��Ӧ�IJ����ֱ�Ϊt1��t2����t1+t2=$\sqrt{3}$��t1t2=-3��
��|MA|+|MB|=|t1|+|t2|=|t1-t2|=$\sqrt{��{t}_{1}+{t}_{2}��^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{3+12}$=$\sqrt{15}$��
���� ���⿼�����ߵ�ֱ�����귽����ֱ�ߵIJ������̵����������߶κ͵����漰��ֱ�����귽�̡������귽�̡��������̵Ļ�����Τ�ﶨ���Ȼ���֪ʶ������������֤����������������������黯����ת��˼�롢�����뷽��˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overline{x}$=�� | B�� | $\overline{x}$�֦� | C�� | ����$\overline{x}$�Ĺ���ֵ | D�� | $\overline{x}$�Ǧ̵Ĺ���ֵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
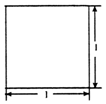 ��һ�������ǵ���ֱ�������ε�ֱ������������ͼ��ͼ��ʾ���䶥�㶼��һ�������ϣ������ı����Ϊ��������
��һ�������ǵ���ֱ�������ε�ֱ������������ͼ��ͼ��ʾ���䶥�㶼��һ�������ϣ������ı����Ϊ��������| A�� | 6�л�5�� | B�� | 3�л�5�� | C�� | 6�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֱ�� | B�� | Բ | C�� | ��Բ | D�� | ˫���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2\sqrt{2}}{3}$��$\frac{4\sqrt{2}}{9}$ | B�� | $\frac{\sqrt{2}}{4}$ | C�� | $\frac{7\sqrt{2}}{8}$ | D�� | $\frac{\sqrt{2}}{4}$��$\frac{7\sqrt{2}}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
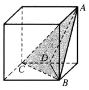 ��ͼ��һ�������壬A��B��CΪ�������㣬D������е㣬������A-BCD������ͼ������ͼ�ǣ�ע��ѡ���е���ͼ������ͼ����ͼ�Ǹ���ͼ����������
��ͼ��һ�������壬A��B��CΪ�������㣬D������е㣬������A-BCD������ͼ������ͼ�ǣ�ע��ѡ���е���ͼ������ͼ����ͼ�Ǹ���ͼ����������| A�� | 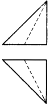 | B�� | 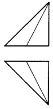 | C�� | 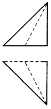 | D�� | 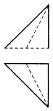 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��?p����q | B�� | p��q | C�� | p�ģ�?q�� | D�� | p�ţ�?q�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com