
已知椭圆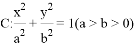 经过点
经过点 ,且离心率为
,且离心率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 是椭圆上的点,直线
是椭圆上的点,直线 与
与 (
( 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为 .若动点
.若动点 满足
满足 ,试探究是否存在两个定点
,试探究是否存在两个定点 ,使得
,使得 为定值?若存在,求
为定值?若存在,求 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
科目:高中数学 来源:2017届广西柳州市、钦州市高三第一次模拟考试数学(理)试卷(解析版) 题型:解答题
已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届湖北省七市(州)高三第一次联合调考(3月联考)数学(理)试卷(解析版) 题型:选择题
在正数数列 中,
中, ,且点
,且点 在直线
在直线 上, 则
上, 则 的前
的前 项和
项和 等于( )
等于( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2017届甘肃省兰州市高三第一次诊断性考试数学(理)试卷(解析版) 题型:填空题
已知在三棱锥 中,
中, ,
,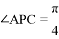 ,
, ,
, ,
, ,且平面
,且平面 平面
平面 ,那么三棱锥
,那么三棱锥 外接球的体积为__________.
外接球的体积为__________.
查看答案和解析>>
科目:高中数学 来源:2017届甘肃省兰州市高三第一次诊断性考试数学(理)试卷(解析版) 题型:选择题
如图中的程序框图的算法思路来源于我国古代数学名著《九章算法》中的“更相减损术”,执行该程序框图,若输入 的值分别为
的值分别为 ,则输入的
,则输入的 ( )
( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:解答题
某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为 .
.
(1)若出现故障的机器台数为 ,求
,求 的分布列;
的分布列;
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com