Question

19．△ABC中，D为边BC上的一点，BD=33，sinB=$\frac{5}{13}$，cos∠ADC=$\frac{3}{5}$，则AD为25．

Answer 1

分析 先由cos∠ADC=$\frac{3}{5}$确定角ADC的范围，因为∠BAD=∠ADC-B所以可求其正弦值，最后由正弦定理可得答案．

解答 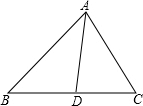解：由cos∠ADC=$\frac{3}{5}$＞0，则∠ADC＜$\frac{π}{2}$，
又由知B＜∠ADC可得B＜$\frac{π}{2}$，
由sinB=$\frac{5}{13}$，可得cosB=$\frac{12}{13}$，
又由cos∠ADC=$\frac{3}{5}$，可得sin∠ADC=$\frac{4}{5}$．
从而sin∠BAD=sin（∠ADC-B）=sin∠ADCcosB-cos∠ADCsinB=$\frac{4}{5}$×$\frac{12}{13}-\frac{3}{5}×\frac{5}{13}$=$\frac{33}{65}$．
由正弦定理得 $\frac{AD}{sinB}$=$\frac{BD}{sin∠BAD}$，
所以AD=$\frac{BD•sinB}{sin∠BAD}$=$\frac{33×\frac{5}{13}}{\frac{33}{65}}$=25．
故答案为：25．

点评 三角函数与解三角形的综合性问题，是近几年高考的热点，在高考试题中频繁出现．这类题型难度比较低，一般出现在17或18题，属于送分题，估计以后这类题型仍会保留，不会有太大改变．解决此类问题，要根据已知条件，灵活运用正弦定理或余弦定理，求边角或将边角互化，属于基础题．