
ΓΨΧβΡΩΓΩ…ηaΓΌbΘ§ΫβΙΊ”ΎxΒΡ≤ΜΒ» Ϋa2xΘΪb2(1Θ≠x)Γί[axΘΪb(1Θ≠x)]2Θ°
ΓΨ¥πΑΗΓΩ{x|0ΓήxΓή1}Θ°
ΓΨΫβΈωΓΩ
ΫΪ‘≠≤ΜΒ» ΫΜ·ΦρΈΣ(aΘ≠b)2(x2Θ≠x) Γή0Θ§”…ΧθΦΰΒΟΒΫœΒ ΐ(aΘ≠b)2ΘΨ0Θ§÷±Ϋ”Ϋβ≥ω≤ΜΒ» Ϋx2Θ≠xΓή0Φ¥Ω….
ΫβΘΚΫΪ‘≠≤ΜΒ» ΫΜ·ΈΣ
(a2Θ≠b2)x+b2Γί(aΘ≠b)2x2ΘΪ2(aΘ≠b)bxΘΪb2Θ§
“ΤœνΘ§’ϊάμΚσΒΟ (aΘ≠b)2(x2Θ≠x) Γή0Θ§Γ≠
ΓΏ aΓΌb Φ¥ (aΘ≠b)2ΘΨ0Θ§
Γύ x2Θ≠xΓή0Θ§
Φ¥ x(xΘ≠1) Γή0Θ°
Ϋβ¥Υ≤ΜΒ» ΫΘ§ΒΟΫβΦ· {x|0ΓήxΓή1}Θ°
ΓΨΒψΨΠΓΩ
±Ψ–ΓΧβ÷ς“ΣΩΦ≤ι≤ΜΒ» ΫΜυ±Ψ÷Σ ΕΘ§≤ΜΒ» ΫΒΡΫβΖ®ΘΜΫβΧβ ±“ΣΉΔ“βΙΪ ΫΒΡΝιΜν‘Υ”ΟΘ°Ε‘”ΎΚ§≤ΈΒΡΕΰ¥Έ≤ΜΒ» ΫΈ ΧβΘ§œ»≈–ΕœΕΰ¥ΈœνœΒ ΐ «ΖώΚ§≤ΈΘ§Ϋ”Ή≈Χ÷¬έ≤Έ ΐΒ»”Ύ0Θ§≤ΜΒ»”Ύ0Θ§‘ΌΩ¥ ΫΉ”ΡήΖώ“ρ ΫΖ÷ΫβΘ§»τΡήΙΜ“ρ ΫΖ÷Ϋβ‘ρΫχ––Ζ÷ΫβΘ§‘Ό±»ΫœΝΫΗυ¥σ–Γ,ΫαΚœΆΦœώΒΟΒΫ≤ΜΒ» ΫΒΡΫβΦ·.
ΓΨΧβ–ΆΓΩΫβ¥πΧβ
ΓΨΫα χΓΩ
19
ΓΨΧβΡΩΓΩ…ηSn «Β»≤ν ΐΝ–{an}ΒΡ«ΑnœνΚΆΘ§“―÷Σ![]() ”κ
”κ![]() ΒΡΒ»±»÷–œνΈΣ
ΒΡΒ»±»÷–œνΈΣ![]() Θ§«“
Θ§«“![]() ”κ
”κ![]() ΒΡΒ»≤ν÷–œνΈΣ1Θ§«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΓΘ
ΒΡΒ»≤ν÷–œνΈΣ1Θ§«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΓΘ
ΓΨ¥πΑΗΓΩ![]() Μρ
Μρ![]() .
.
ΓΨΫβΈωΓΩ
…ηΒ»≤ν ΐΝ–{an}ΒΡ ΉœνΈΣa1Θ§ΙΪ≤νΈΣdΘ§‘Υ”ΟΒ»≤ν÷–œνΚΆΒ»±»÷–œνΒΡΕ®“εΘ§άϊ”ΟΒ»≤ν ΐΝ–ΒΡ«σΚΆΙΪ ΫΘ§¥ζ»κΩ…«σa1Θ§dΘ§ΫβΖΫ≥ΧΩ…«σΆ®œνanΘ°
…ηΒ»≤ν ΐΝ–{an}ΒΡ Ήœν![]() ,ΙΪ≤νΈΣ
,ΙΪ≤νΈΣ![]() Θ§‘ρΆ®œνΈΣ
Θ§‘ρΆ®œνΈΣ![]() Θ§
Θ§
«Α![]() œνΚΆΈΣ
œνΚΆΈΣ![]() Θ§“άΧβ“β”–
Θ§“άΧβ“β”–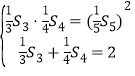 ,
,
Τδ÷–![]() Θ§”…¥ΥΩ…ΒΟ
Θ§”…¥ΥΩ…ΒΟ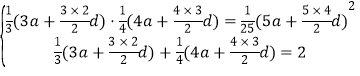 ,
,
’ϊάμΒΟ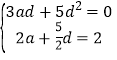 , ΫβΖΫ≥ΧΉιΒΟ
, ΫβΖΫ≥ΧΉιΒΟ![]() Μρ
Μρ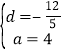 ,
,
”…¥ΥΒΟ![]() ΘΜΜρ
ΘΜΜρ![]() .
.
Ψ≠Φλ―ι![]() ΚΆ
ΚΆ![]() ΨυΚœΧβ“β.
ΨυΚœΧβ“β.
Υυ“‘Υυ«σΒ»≤ν ΐΝ–ΒΡΆ®œνΙΪ ΫΈΣ![]() Μρ
Μρ![]() .
.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ“Μ¥ΈΩΙΚι«άœ’÷–Θ§ΉΦ±Η”Ο…δΜςΒΡΖΫΖ®“ΐ±§¥”«≈…œ”ΈΤ·ΝςΕχœ¬ΒΡ“ΜΗωΨό¥σΒΡΤϊ”ΆΙύΘ§“―÷Σ÷Μ”–5ΖΔΉ”Β·Θ§ΒΎ“Μ¥ΈΟϋ÷–÷ΜΡή ΙΤϊ”ΆΝς≥ωΘ§ΒΎΕΰ¥ΈΟϋ÷–≤≈Ρή“ΐ±§Θ°ΟΩ¥Έ…δΜςœύΜΞΕάΝΔΘ§«“Οϋ÷–Η≈¬ ΕΦ «![]() Θ§«σΘ®1Θ©”ΆΙό±Μ“ΐ±§ΒΡΗ≈¬ ΘΜΘ®2Θ©»γΙϊ“ΐ±§ΜρΉ”Β·¥ρΙβ‘ρΆΘ÷Ι…δΜςΘ§…η…δΜς¥Έ ΐΈΣ
Θ§«σΘ®1Θ©”ΆΙό±Μ“ΐ±§ΒΡΗ≈¬ ΘΜΘ®2Θ©»γΙϊ“ΐ±§ΜρΉ”Β·¥ρΙβ‘ρΆΘ÷Ι…δΜςΘ§…η…δΜς¥Έ ΐΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡΖ÷≤ΦΝ–Θ°
ΒΡΖ÷≤ΦΝ–Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕ![]() ÷–Θ§
÷–Θ§ ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§ ![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ§
ΒΡ÷–ΒψΘ§ ![]() Θ§
Θ§ ![]() .
.
Θ®1Θ©÷ΛΟςΘΚ ![]() ΤΫΟφ
ΤΫΟφ![]() .
.
Θ®2Θ©÷ΛΟςΘΚ ![]() ΤΫΟφ
ΤΫΟφ![]() .
.
Θ®3Θ©«σ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…ΒΡΫ«ΒΡ’ΐ«–÷Β.
Υυ≥…ΒΡΫ«ΒΡ’ΐ«–÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ ![]() ΓΘ
ΓΘ
Θ®1Θ©«σΚ· ΐ![]() ΒΡΕ®“ε”ρΚΆ÷Β”ρΘΜ
ΒΡΕ®“ε”ρΚΆ÷Β”ρΘΜ
Θ®2Θ©…η![]() Θ®
Θ®![]() ΈΣ Β ΐΘ©Θ§«σ
ΈΣ Β ΐΘ©Θ§«σ![]() ‘Ύ
‘Ύ![]() ±ΒΡΉν¥σ÷Β
±ΒΡΉν¥σ÷Β![]() ΘΜ
ΘΜ
Θ®3Θ©Ε‘Θ®2Θ©÷–![]() Θ§»τ
Θ§»τ![]() Ε‘
Ε‘![]() Υυ”–ΒΡ Β ΐ
Υυ”–ΒΡ Β ΐ![]() ΦΑ
ΦΑ![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΓΘ
ΒΡ»Γ÷ΒΖΕΈßΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΒΟΒΫΚ· ΐy=sinΘ®2x©¹ ![]() Θ©ΒΡΆΦœσΘ§÷Μ–ηΑ―Κ· ΐy=sinΘ®2x+
Θ©ΒΡΆΦœσΘ§÷Μ–ηΑ―Κ· ΐy=sinΘ®2x+ ![]() Θ©ΒΡΆΦœσΘ® Θ©
Θ©ΒΡΆΦœσΘ® Θ©
A.œρΉσΤΫ“Τ ![]() Ηω≥ΛΕ»ΒΞΈΜ
Ηω≥ΛΕ»ΒΞΈΜ
B.œρ”“ΤΫ“Τ ![]() Ηω≥ΛΕ»ΒΞΈΜ
Ηω≥ΛΕ»ΒΞΈΜ
C.œρΉσΤΫ“Τ ![]() Ηω≥ΛΕ»ΒΞΈΜ
Ηω≥ΛΕ»ΒΞΈΜ
D.œρ”“ΤΫ“Τ ![]() Ηω≥ΛΕ»ΒΞΈΜ
Ηω≥ΛΕ»ΒΞΈΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®±Ψ–ΓΧβ10Ζ÷Θ©―Γ–ό4ΓΣ4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
“―÷Σ«ζœΏC1ΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() Θ®tΈΣ≤Έ ΐΘ©Θ§“‘Ήχ±ξ‘≠ΒψΈΣΦΪΒψΘ§x÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏC2ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣΠ―=2sinΠ»ΓΘ
Θ®tΈΣ≤Έ ΐΘ©Θ§“‘Ήχ±ξ‘≠ΒψΈΣΦΪΒψΘ§x÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏC2ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣΠ―=2sinΠ»ΓΘ
Θ®ΔώΘ©Α―C1ΒΡ≤Έ ΐΖΫ≥ΧΜ·ΈΣΦΪΉχ±ξΖΫ≥ΧΘΜ
Θ®ΔρΘ©«σC1”κC2ΫΜΒψΒΡΦΪΉχ±ξΘ®Π―Γί0,0ΓήΠ»ΘΦ2Π–Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘Ύ÷±Ϋ«Ήχ±ξœΒxOy÷–,«ζœΏCΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() (Π»ΈΣ≤Έ ΐ),÷±œΏlΨ≠ΙΐΕ®ΒψP(3,5),«ψ–±Ϋ«ΈΣ
(Π»ΈΣ≤Έ ΐ),÷±œΏlΨ≠ΙΐΕ®ΒψP(3,5),«ψ–±Ϋ«ΈΣ![]() .
.
(1)–¥≥ω÷±œΏlΒΡ≤Έ ΐΖΫ≥ΧΚΆ«ζœΏCΒΡ±ξΉΦΖΫ≥Χ.
(2)…η÷±œΏl”κ«ζœΏCœύΫΜ”ΎA,BΝΫΒψ,«σ|PA|ΓΛ|PB|ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=xlnx+ ![]() mx2©¹Θ®m+1Θ©x+1Θ°
mx2©¹Θ®m+1Θ©x+1Θ°
Θ®1Θ©»τgΘ®xΘ©=f'Θ®xΘ©Θ§Χ÷¬έgΘ®xΘ©ΒΡΒΞΒς–‘ΘΜ
Θ®2Θ©»τfΘ®xΘ©‘Ύx=1¥Π»ΓΒΟΦΪ–Γ÷ΒΘ§«σ Β ΐmΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
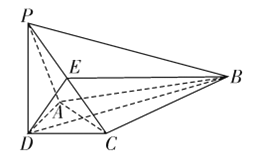
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎPΒΊ’ΐΈςΖΫœρ8kmΒΡA¥ΠΚΆ’ΐΕΪΖΫœρ1kmΒΡB¥ΠΗς”–“ΜΧθ’ΐ±±ΖΫœρΒΡΙΪ¬ΖACΚΆBDΘ§œ÷ΦΤΜ°‘ΎACΚΆBD¬Ζ±ΏΗς–όΫ®“ΜΗωΈοΝς÷––ΡEΚΆFΘ§ΈΣΜΚΫβΫΜΆ®―ΙΝΠΘ§ΨωΕ®–όΫ®ΝΫΧθΜΞœύ¥Ι÷±ΒΡΙΪ¬ΖPEΚΆPFΘ§…ηΓœEPA=ΠΝΘ®0ΘΦΠΝΘΦ ![]() Θ©Θ°
Θ©Θ° 
Θ®1Θ©ΈΣΦθ…ΌΕ‘÷ή±Ώ«χ”ρΒΡ”ΑœλΘ§ ‘»ΖΕ®EΘ§FΒΡΈΜ÷ΟΘ§ ΙΓςPAE”κΓςPFBΒΡΟφΜΐ÷°ΚΆΉν–ΓΘΜ
Θ®2Θ©ΈΣΫΎ ΓΫ®…η≥…±ΨΘ§ ‘»ΖΕ®EΘ§FΒΡΈΜ÷ΟΘ§ ΙPE+PFΒΡ÷ΒΉν–ΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com