
【题目】若椭圆![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() :
:![]() (
(![]() )的焦距相等,给出如下四个结论:
)的焦距相等,给出如下四个结论:
①![]() 和
和![]() 一定有交点;
一定有交点;
②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ;
;
④设![]() 与
与![]() 在第一象限内相交于点
在第一象限内相交于点![]() ,若
,若![]() ,则
,则![]() .
.
其中,所有正确结论的序号是______.
【答案】②④
【解析】
通过![]() 时的图像可知
时的图像可知![]() 和
和![]() 没有交点,根据两椭圆
没有交点,根据两椭圆![]() 相同,结合
相同,结合![]() ,得到
,得到![]() ,根据
,根据![]() 分析法得到所需条件与
分析法得到所需条件与![]() 矛盾,根据椭圆对称性,结合
矛盾,根据椭圆对称性,结合![]() 得到两椭圆之间离心率的关系,从而得到
得到两椭圆之间离心率的关系,从而得到![]() .
.
对于结论①,当![]() 时,椭圆
时,椭圆![]() 的图像完全在椭圆
的图像完全在椭圆![]() 的内部,
的内部,
此时![]() 和
和![]() 没有交点,所以①错误;
没有交点,所以①错误;
对于结论②,因为两椭圆的焦距相等,即![]() 相等,可得
相等,可得![]() ,
,
因为![]() ,所以得到
,所以得到![]()
由![]() 可得
可得![]() ,
,
所以得到![]() ,
,
所以得到![]() ,所以②正确;
,所以②正确;
对于结论③,由![]() 可得
可得![]() ,
,
即![]() ,即
,即![]() ,
,
从而得到![]() ,与条件中的
,与条件中的![]() 矛盾,
矛盾,
所以③错误;
对于结论④,因为两椭圆的![]() 相同,若两椭圆的离心率相同,
相同,若两椭圆的离心率相同,
则根据对称性可知,两椭圆在第一象限的交点,其横纵坐标应相等,
而此时![]() 与
与![]() 在第一象限内相交于点
在第一象限内相交于点![]() ,
,![]() ,
,
则椭圆![]() 更接近圆,或椭圆
更接近圆,或椭圆![]() 更扁,即
更扁,即![]() ,
,
所以![]() ,得到
,得到![]() ,
,
所以④正确.
故答案为:②④.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:
【题目】如图所示在四棱锥![]() 中,下底面
中,下底面![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() ,
,![]() 为以
为以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() ,若点
,若点![]() 是线段
是线段![]() 上的中点.
上的中点.
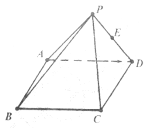
(1)证明![]() 平面
平面![]() .
.
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年时红军长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神.首先在甲、乙、丙、丁四个不同的公园进行支持签名活动.
公园 | 甲 | 乙 | 丙 | 丁 |
获得签名人数 | 45 | 60 | 30 | 15 |
然后在各公园签名的人中按分层抽样的方式抽取10名幸运之星回答问题,从10个关于长征的问题中随机抽取4个问题让幸运之星回答,全部答对的幸运之星获得一份纪念品.
(Ⅰ)求此活动中各公园幸运之星的人数;
(Ⅱ)若乙公园中每位幸运之星对每个问题答对的概率均为![]() ,求恰好2位幸运之星获得纪念品的概率;
,求恰好2位幸运之星获得纪念品的概率;
(Ⅲ)若幸运之星小李对其中8个问题能答对,而另外2个问题答不对,记小李答对的问题数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,两直角边AB,AC的长分别为m,n(其中
中,两直角边AB,AC的长分别为m,n(其中![]() ),以BC的中点O为圆心,作半径为r(
),以BC的中点O为圆心,作半径为r(![]() )的圆O.
)的圆O.

(1)若圆O与![]() 的三边共有4个交点,求r的取值范围;
的三边共有4个交点,求r的取值范围;
(2)设圆O与边BC交于P,Q两点;当r变化时,甲乙两位同学均证明出![]() 为定值甲同学的方法为:连接AP,AQ,AO,利用两个小三角形中的余弦定理来推导;乙同学的方法为;以O为原点建立合适的直角坐标系,利用坐标法来计算.请在甲乙两位同学的方法中选择一种来证明该结论,定值用含m、n的式子表示.(若用两种方法,按第一种方法给分)
为定值甲同学的方法为:连接AP,AQ,AO,利用两个小三角形中的余弦定理来推导;乙同学的方法为;以O为原点建立合适的直角坐标系,利用坐标法来计算.请在甲乙两位同学的方法中选择一种来证明该结论,定值用含m、n的式子表示.(若用两种方法,按第一种方法给分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:①![]() 都是不等于
都是不等于![]() 的实数,关于
的实数,关于![]() 的不等式和
的不等式和![]() 的解集分别为
的解集分别为![]() ,则当
,则当![]() 是
是![]() 的既不充分也不必要条件;②
的既不充分也不必要条件;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .其中正确的个数为( )
.其中正确的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com