
已知椭圆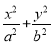 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为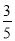 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,

过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
(1)求椭圆方程;
(2)若圆N与x轴相切,求圆N的方程;
(3)设点R为圆N上的动点,点R到直线PF的最大距离为d,求d的取值范围.
(1)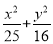 =1(2)
=1(2)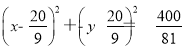 (3)
(3)
【解析】(1)∵e=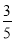 不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为
不妨设c=3k,a=5k,则b=4k,其中k>0,故椭圆方程为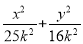 =1(a>b>0),∵P
=1(a>b>0),∵P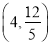 在椭圆上,∴
在椭圆上,∴ =1解得k=1,∴椭圆方程为
=1解得k=1,∴椭圆方程为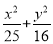 =1.
=1.
(2)kAP= ,则直线AP的方程为y=-
,则直线AP的方程为y=-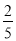 x+4,
x+4,
令y=t ,则x=
,则x= ∴M
∴M .∵Q(0,t)∴N
.∵Q(0,t)∴N ,
,
∵圆N与x轴相切,∴ =t,由题意M为第一象限的点,则
=t,由题意M为第一象限的点,则 =t,解得t=
=t,解得t=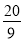 .∴N
.∴N ,圆N的方程为
,圆N的方程为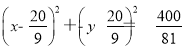 .
.
(3)F(3,0),kPF=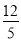 ,∴直线PF的方程为y=
,∴直线PF的方程为y= (x-3)即12x-5y-36=0,
(x-3)即12x-5y-36=0,
∴点N到直线PF的距离为 ,
,
∴d=
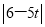 +
+ (4-t),∵0<t<4,
(4-t),∵0<t<4,
∴当0<t≤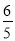 时,d=
时,d=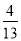 (6-5t)+
(6-5t)+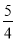 (4-t)=
(4-t)=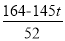 ,此时
,此时 ≤d<
≤d< ,
,
当 <t<4时,d=
<t<4时,d= (5t-6)+
(5t-6)+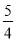 (4-t)=
(4-t)=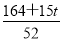 ,此时
,此时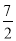 <d<
<d<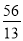 ,
,
∴综上,d的取值范围为 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第4课时练习卷(解析版) 题型:解答题
若方程ax2+ay2-4(a-1)x+4y=0表示圆,求实数a的取值范围,并求出半径最小的圆的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第3课时练习卷(解析版) 题型:填空题
已知直线l:y=3x+3,那么直线x-y-2=0关于直线l对称的直线方程为____________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:解答题
如图,已知梯形ABCD中|AB|=2|CD|,点E满足 =λ
=λ ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当 ≤λ≤
≤λ≤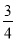 时,求双曲线离心率e的取值范围.
时,求双曲线离心率e的取值范围.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第11课时练习卷(解析版) 题型:填空题
已知椭圆C: +y2=1的两焦点为F1,F2,点P(x0,y0)满足
+y2=1的两焦点为F1,F2,点P(x0,y0)满足 +
+ ≤1,则PF1+PF2的取值范围为________.
≤1,则PF1+PF2的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:解答题
给定椭圆C: =1(a>b>0),称圆心在原点O、半径是
=1(a>b>0),称圆心在原点O、半径是 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F(
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F( ,0),其短轴的一个端点到点F的距离为
,0),其短轴的一个端点到点F的距离为 .
.
(1)求椭圆C和其“准圆”的方程;
(2)若点A是椭圆C的“准圆”与x轴正半轴的交点,B、D是椭圆C上的两相异点,且BD⊥x轴,求 ·
· 的取值范围;
的取值范围;
(3)在椭圆C的“准圆”上任取一点P,过点P作直线l1,l2,使得l1,l2与椭圆C都只有一个交点,试判断l1,l2是否垂直?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第九章第10课时练习卷(解析版) 题型:解答题
如图,F是中心在原点、焦点在x轴上的椭圆C的右焦点,直线l:x=4是椭圆C的右准线,F到直线l的距离等于3.

(1)求椭圆C的方程;
(2)点P是椭圆C上动点,PM⊥l,垂足为M.是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西工大附中高三上学期第四次适应性训练理数学卷(解析版) 题型:填空题
已知 是
是 椭圆的一个焦点,
椭圆的一个焦点, 是短轴的一个端点,线段
是短轴的一个端点,线段 的延长线交
的延长线交 于点
于点 ,且
,且 ,则
,则 的离心率为 .
的离心率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安铁一中国际合作学校高三下第一次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求函数的定义域;(2)判断函数 的奇偶性;(3)求证:
的奇偶性;(3)求证: ﹥0.
﹥0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com