
分析 (1)由已知得b=c,$\sqrt{{a}^{2}+{b}^{2}}$=2$\sqrt{3}$,由此能求出椭圆方程.
(2)由(1)得F(2,0),0≤m≤2,设l的方程为y=k(x-2),代入$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1,得(2k2+1)x2-8k2x+8k2-8=0,由此利用韦达定理、中点坐标公式、直线垂直,结合已知条件能求出结果.
解答 解:(1)∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的半焦距为c,且b=c,椭圆的上顶点到右顶点的距离为2$\sqrt{3}$,
∴$\left\{\begin{array}{l}{b=c}\\{\sqrt{{a}^{2}+{b}^{2}}=2\sqrt{3}}\\{{b}^{2}+{c}^{2}={a}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2\sqrt{2}}\\{c=2}\\{b=2}\end{array}\right.$,
∴椭圆方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1.
(2)由(1)得F(2,0),∴0≤m≤2,
假设存在满足题意的直线l,则直线l的斜率存在,设为k,
则l的方程为y=k(x-2),代入$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1,得(2k2+1)x2-8k2x+8k2-8=0,
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{2{k}^{2}+1}$,${x}_{1}{x}_{2}=\frac{8{k}^{2}-8}{2{k}^{2}+1}$,
∴y1+y2=k(x1+x2-4)=$\frac{-4k}{2{k}^{2}+1}$,
设AB的中点为M,则M($\frac{4{k}^{2}}{2{k}^{2}+1}$,-$\frac{2k}{2{k}^{2}+1}$),
∵|AC|=|BC|,∴CM⊥AB,∴kCM•kAB=-1,
∴$\frac{\frac{-2k}{2{k}^{2}+1}}{\frac{4{k}^{2}}{2{k}^{2}+1}-m}$•k=-1,化简,得${k}^{2}=\frac{m}{2(1-m)}$,
当0≤m<1时,k=$±\sqrt{\frac{m}{2-2m}}$,即存在这样的直线l满足条件,
当l≤m≤2时,k不存在,即不存在这样的直线l满足条件.
点评 本题考查椭圆方程的求法,考查满足条件的直线是否存在的判断与求法,是中档题,解题时要认真审题,注意韦达定理、中点坐标公式、直线垂直的性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A与B对立 | B. | A与C对立 | ||
| C. | B与C互斥 | D. | 任何两个事件均不互斥 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示:四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:
如图所示:四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
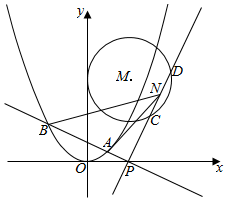 如图,抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切.
如图,抛物线E:x2=2py(p>0)的焦点为$(0,\frac{1}{4})$,圆心M在射线y=2x(x≥0)上且半径为1的圆M与y轴相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com