
【题目】已知函数f(x)=xlnx﹣ax2+ ![]() .
.
(I) 当a= ![]() 时,判断f(x)在其定义上的单调性;
时,判断f(x)在其定义上的单调性;
(Ⅱ)若函数f(x)有两个极值点x1 , x2 , 其中x1<x2 . 求证:
(i)f(x2)>0;
(ii)x1+x2> ![]() .
.
【答案】解:(Ⅰ)函数f(x)的定义域是(0,+∞),
a= ![]() 时,f(x)=xlnx﹣
时,f(x)=xlnx﹣ ![]() x2+
x2+ ![]() ,f′(x)=lnx+1﹣x,f″(x)=
,f′(x)=lnx+1﹣x,f″(x)= ![]() ,
,
当0<x<1时,f″(x)>0,当x>1时,f″(x)<0,
∴f′(x)在(0,1)递增,在(1,+∞)递减,
∴f′(x)max=f′(1)=0,
∴f′(x)≤0,f(x)在(0,+∞)递减;
(Ⅱ)证明:(i)∵f′(x)=lnx+1﹣2ax,
∴由函数f(x)有两个极值点x1 , x2
得函数f′(x)=lnx+1﹣2ax,x>0有两个零点x1 , x2
∵f″(x)= ![]() ﹣2a=
﹣2a= ![]() ,
,
当a≤0时,有f″(x)>0此时f′(x)在x∈(0,+∞)上单调递增,
∴不符合,
∴a>0此时x∈(0, ![]() )时,f″(x)>0,x∈(
)时,f″(x)>0,x∈( ![]() ,+∞)时,f″(x)<0
,+∞)时,f″(x)<0
∴f′(x)在x∈(0, ![]() )上单调递增,在x∈(
)上单调递增,在x∈( ![]() ,+∞)上单调递减
,+∞)上单调递减
又f′(x)有两个零点x1 , x2 ,
∴f′( ![]() )>0,∴ln
)>0,∴ln ![]() >0,∴
>0,∴ ![]() >1,∴0<a<
>1,∴0<a< ![]() ,
,
∴当x∈(0,x1)时,f′(x)<0,当x∈(x1 , x2)时,f′(x)>0,
当x∈(x2 , +∞)时,f′(x)<0
∴f(x)在x∈(0,x1)上单调递减,在x∈(x1 , x2)上单调递增,
在x∈(x2 , +∞)上单调递减
又f′(1)=1﹣2a>0,∴1∈(x1 , x2)
∴f(x2)>f(1)=﹣a+ ![]() >0;
>0;
(ii)由(i)得:0<a< ![]() ,
,
且lnx1+1=2ax1 , lnx2+1=2ax2 ,
∴lnx1+lnx2+2=2a(x1+x2),
lnx1﹣lnx2=2a(x1﹣x2),
∴ln(x1x2)+2= ![]() ln
ln ![]() ,
,
令t= ![]() ,则0<t<1,且lnx1x2+2=
,则0<t<1,且lnx1x2+2= ![]() lnt…①,
lnt…①,
而lnx1+lnx2+2=2a(x1+x2)…②,
由①②,可得x1+x2> ![]() 2a(x1+x2)>2
2a(x1+x2)>2
lnx1+lnx2+2>2 ![]() lnt>2
lnt>2
lnt< ![]() lnt﹣
lnt﹣ ![]() <0,
<0,
下面证明:当t∈(0,1)时,lnt﹣ ![]() <0,
<0,
令h(t)=lnt﹣ ![]() ,h′(t)=
,h′(t)=  >0,
>0,
∴h(t)在(0,1)递增,h(t)<h(1)=0,
∴lnt﹣ ![]() <0,
<0,
∴x1+x2> ![]() .
.
【解析】(Ⅰ)求出f(x)的导数,得到导函数的单调性,求出f′(x)max=f′(1)=0,从而求出函数f(x)的单调性;(Ⅱ)(i)函数f'(x)=lnx+1﹣2ax,x>0有两个零点x1 , x2 , 讨论a>0,a≤0,再求导数,得到f′( ![]() )>0,从而0<a<
)>0,从而0<a< ![]() ,再讨论f(x)的单调性,即可得证;(ii)得到ln(x1x2)+2=
,再讨论f(x)的单调性,即可得证;(ii)得到ln(x1x2)+2= ![]() ln
ln ![]() ,令t=
,令t= ![]() ,问题转化为证明lnt﹣
,问题转化为证明lnt﹣ ![]() <0在(0,1)恒成立,根据函数的单调性证明即可.
<0在(0,1)恒成立,根据函数的单调性证明即可.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的极值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinx﹣ ![]() cosx(a∈R)的图象经过点(
cosx(a∈R)的图象经过点( ![]() ,0).
,0).
(1)求f(x)的最小正周期;
(2)若x∈[ ![]() ,
, ![]() ],求f(x)的取值范围.
],求f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() (a>0,且a≠1)的值域为(﹣∞,+∞),则实数a的取值范围是( )
(a>0,且a≠1)的值域为(﹣∞,+∞),则实数a的取值范围是( )
A.(3,+∞)
B.(0, ![]() ]
]
C.(1,3)
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱ABC﹣A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为 ![]() ,且∠AA1C1为锐角.
,且∠AA1C1为锐角.
(I) 求证:AA1⊥BC1;
(Ⅱ)求锐二面角B﹣AC﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三一班举办消防安全知识竞赛,分别选出3名男生和3名女生组成男队和女队,每人一道必答题,答对则为本队得10分,答错与不答都得0分,已知男队每人答对的概率依次为 ![]() ,
, ![]() ,
, ![]() ,女队每人答对的概率都是
,女队每人答对的概率都是 ![]() ,设每人回答正确与否相互之间没有影响,用X表示男队的总得分.
,设每人回答正确与否相互之间没有影响,用X表示男队的总得分.
(I) 求X的分布列及其数学期望E(X);
(Ⅱ)求在男队和女队得分之和为50的条件下,男队比女队得分高的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( ) 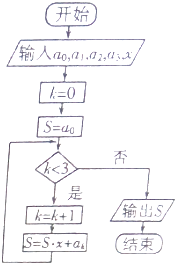
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m>0,p:(x+2)(x-6)≤0,q:2-m≤x≤2+m.
(1)若p是q成立的必要不充分条件,求实数m的取值范围;
(2)若![]() 是
是![]() 成立的充分不必要条件,求实数m的取值范围.
成立的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com