
分析 (1)由(n+1)an=2Sn,可得${S_n}=\frac{{({n+1}){a_n}}}{2}$,n∈N*,利用递推关系可得:$\frac{a_n}{{{a_{n-1}}}}=\frac{n}{n-1}$( n≥2).利用“累乘求积”方法即可得出an.利用等比数列的通项公式即可得出bn.
(2)由anbn=n$•(\frac{1}{2})^{n}$,利用“错位相减法”与等比数列的求和公式即可得出Tn.代入不等式λnTn+2bnSn<2(λn+3bn),化简整理利用二次函数的单调性即可得出.
解答 解:(1)∵(n+1)an=2Sn,∴${S_n}=\frac{{({n+1}){a_n}}}{2}$,n∈N*
当n≥2时,${a_n}={S_n}-{S_{n-1}}=\frac{{({n+1}){a_n}}}{2}-\frac{{n{a_{n-1}}}}{2}$,
∴nan-1=(n-1)an,即$\frac{a_n}{{{a_{n-1}}}}=\frac{n}{n-1}$( n≥2).
∴${a_n}=\frac{a_n}{{{a_{n-1}}}}•\frac{{{a_{n-1}}}}{{{a_{n-2}}}}…\frac{a_3}{a_2}•\frac{a_2}{a_1}•{a_1}=\frac{n}{n-1}•\frac{n-1}{n-2}•\frac{n-2}{n-3}…\frac{3}{2}•\frac{2}{1}•1=n$(n≥2),
又a1=1,也满足上式,
故数列{an}的通项公式an=n(n∈N*)..
由$b_{n+1}^2={b_n}•{b_{n+2}},且{b_1}≠0$,${b_1}=\frac{1}{2}$,${b_2}=\frac{1}{4}$,
可知:数列{bn}是等比数列,其首项、公比均为$\frac{1}{2}$,
∴数列{bn}的通项公式:bn=$(\frac{1}{2})^{n}$.
(2)∵anbn=n$•(\frac{1}{2})^{n}$.
∴Tn=$\frac{1}{2}+2×(\frac{1}{2})^{2}$+3×$(\frac{1}{2})^{3}$+…+n$•(\frac{1}{2})^{n}$.
$\frac{1}{2}{T}_{n}$=$(\frac{1}{2})^{2}+2×(\frac{1}{2})^{3}$+…+(n-1)$•(\frac{1}{2})^{n}$+n$•(\frac{1}{2})^{n+1}$,
∴$\frac{1}{2}$Tn=$\frac{1}{2}+(\frac{1}{2})^{2}$+…+$(\frac{1}{2})^{n}$-n$•(\frac{1}{2})^{n+1}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-n$•(\frac{1}{2})^{n+1}$,
∴${T_n}=2-\frac{n+2}{2^n}$.
又Sn=1+2+…+n=$\frac{n(n+1)}{2}$.
不等式λnTn+2bnSn<2(λn+3bn)恒成立,
即λn$(2-\frac{n+2}{{2}^{n}})$+$\frac{n(n+1)}{{2}^{n}}$<2$(λn+\frac{3}{{2}^{n}})$,
即(1-λ)n2+(1-2λ)n-6<0,(n∈N*)恒成立.
设f(n)=(1-λ)n2+(1-2λ)n-6,(n∈N*).
当λ=1时,f(n)=-n-6<0恒成立,则λ=1满足条件;
当λ<1时,由二次函数性质知不恒成立;
当λ>1时,由于对称轴x=$\frac{1-2λ}{1-λ}$<0,则f(n)在[1,+∞)上单调递减,
∴f(n)≤f(1)=-3λ-4<0恒成立,则λ>1满足条件,
综上所述,实数λ的取值范围是[1,+∞).
点评 本题考查了数列递推关系、“累乘求积”方法、等比数列的通项公式与求和公式、“错位相减法”、二次函数的单调性、分类讨论方法,考查了推理能力与计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=4,AC=2$\sqrt{7}$,DC=2
如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=4,AC=2$\sqrt{7}$,DC=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
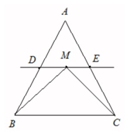 在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.
在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 4π | C. | 5π | D. | 6π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{15}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3\sqrt{15}}{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com