
分析 根据向量数量积的定义结合双曲线的性质进行求解即可.
解答 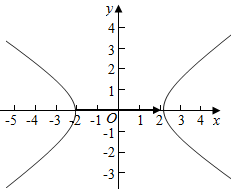 解:由向量数量积的定义知$\overrightarrow{MN}$•$\overrightarrow{v}$即向量$\overrightarrow{MN}$在向量$\overrightarrow{v}$上的投影|$\overrightarrow{v}$|模长的乘积,故求|$\overrightarrow{MN}$•$\overrightarrow{v}$|的最小值,
解:由向量数量积的定义知$\overrightarrow{MN}$•$\overrightarrow{v}$即向量$\overrightarrow{MN}$在向量$\overrightarrow{v}$上的投影|$\overrightarrow{v}$|模长的乘积,故求|$\overrightarrow{MN}$•$\overrightarrow{v}$|的最小值,
即求$\overrightarrow{MN}$在x轴上的投影的绝对值的最小值,
由双曲线的图象可知|$\overrightarrow{MN}$•$\overrightarrow{v}$|的最小值为4
故答案为:4
点评 本题主要考查双曲线性质的应用,根据向量数量积的定义转化为投影关系是解决本题的关键.


科目:高中数学 来源: 题型:解答题
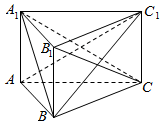 如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面的棱柱为直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°.
如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面的棱柱为直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
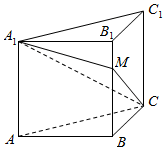 棱长为1的正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
棱长为1的正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 省农科所经过5年对甲、乙两棉种的实验研究,将连续5年棉花产量(千克/亩)的统计数据用茎叶图表示如图,则平均产量较高与产量较稳定的分别是( )
省农科所经过5年对甲、乙两棉种的实验研究,将连续5年棉花产量(千克/亩)的统计数据用茎叶图表示如图,则平均产量较高与产量较稳定的分别是( )| A. | 棉农甲;棉农甲 | B. | 棉农乙;棉农甲 | C. | 棉农甲;棉农乙 | D. | 棉农乙;棉农乙 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com