
【题目】设F为双曲线 ![]() ﹣
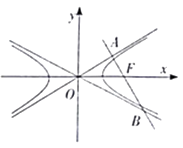
﹣ ![]() =1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( )
=1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( ) 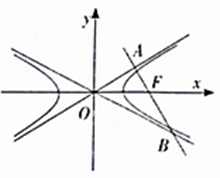
A.![]()
B.2
C.![]()
D.![]()
【答案】C
【解析】解:不妨设OA的倾斜角为锐角,
∵a>b>0,即0< ![]() <1,
<1,
∴渐近线l1的倾斜角为(0, ![]() ),
),
∴ ![]() =
= ![]() =e2﹣1<1,
=e2﹣1<1,
∴1<e2<2,
∵2|AB|=|OA|+|OB|,OA⊥AB,
∴|AB|2=|OB|2﹣|OA|2
=(|OB|﹣|OA|)(|OB|+|OA|)=2(|OB|﹣|OA|)|AB|,
∴|AB|=2(|OB|﹣|OA|),
∴|OB|﹣|OA|= ![]() |AB|,
|AB|,
又|OA|+|OB|=2|AB|,
∴|OA|= ![]() |AB|,
|AB|,
∴在直角△OAB中,tan∠AOB= ![]() =
= ![]() ,
,
由对称性可知:OA的斜率为k=tan( ![]() ∠AOB),
∠AOB),
∴ ![]() =
= ![]() ,∴2k2+3k﹣2=0,
,∴2k2+3k﹣2=0,
∴k= ![]() (k=﹣2舍去);
(k=﹣2舍去);
∴ ![]() =
= ![]() ,∴
,∴ ![]() =
= ![]() =e2﹣1=
=e2﹣1= ![]() ,
,
∴e2= ![]() ,
,
∴e= ![]() .
.
故选:C.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知圆M过点A(1,3),B(4,2),且圆心在直线y=x﹣3上.
(Ⅰ)求圆M的方程;
(Ⅱ)若过点(﹣4,1)的直线l与圆M相切,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
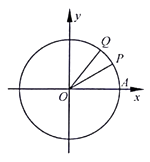
【题目】设A是单位圆O和x轴正半轴的交点,P,Q是圆O上两点,O为坐标原点,∠AOP= ![]() ,∠AOQ=α,α∈[0,
,∠AOQ=α,α∈[0, ![]() ].
]. 
(1)若Q( ![]() ,
, ![]() ),求cos(α﹣
),求cos(α﹣ ![]() )的值;
)的值;
(2)设函数f(α)=sinα( ![]()
![]() ),求f(α)的值域.
),求f(α)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产一种产品的固定成本(即固定投入)为0.5万元,但每生产一百件这样的产品,需要增加可变成本(即另增加投入)0.25万元. 市场对此产品的年需求量为500件,销售的收入函数为![]() =
=![]() (单位:万元),其中
(单位:万元),其中![]() 是产品售出的数量(单位:百件).
是产品售出的数量(单位:百件).
(1)该公司这种产品的年产量为![]() 百件,生产并销售这种产品所得到的利润为当年产量
百件,生产并销售这种产品所得到的利润为当年产量![]() 的函数
的函数![]() ,求
,求![]() ;
;
(2)当年产量是多少时,工厂所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校,在课堂上,李老师请学生画出自行车行进路程s(千米)与行进时间x(秒)的函数图象的示意图,你认为正确的是
A.  B.
B. 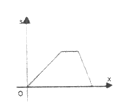
C. 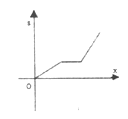 D.
D. 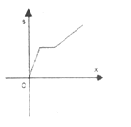
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图C,D是以AB为直径的圆上的两点,![]() ,F是AB上的一点,且
,F是AB上的一点,且![]() ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知![]()

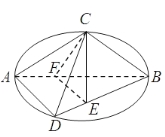
(1)求证:AD![]() 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com