
分析 解2kπ+π≤x-$\frac{π}{3}$≤2kπ+2π可得单调增区间;解x-$\frac{π}{3}$=kπ+$\frac{π}{2}$可得对称中心坐标;解x-$\frac{π}{3}$=kπ可得对称轴方程.
解答 解:∵函数y=cos(x-$\frac{π}{3}$),
由2kπ+π≤x-$\frac{π}{3}$≤2kπ+2π可得2kπ+$\frac{4π}{3}$≤x≤2kπ+$\frac{7π}{3}$,
∴该函数的单调增区间是[2kπ+$\frac{4π}{3}$,2kπ+$\frac{7π}{3}$],k∈Z;
由x-$\frac{π}{3}$=kπ+$\frac{π}{2}$可解得x=kπ+$\frac{5π}{6}$,k∈Z,
∴该函数图象的对称中心坐标是(kπ+$\frac{5π}{6}$,0),k∈Z;
由x-$\frac{π}{3}$=kπ可解得x=kπ+$\frac{π}{3}$,k∈Z,
∴该函数图象的对称轴方程是x=kπ+$\frac{π}{3}$,k∈Z;
故答案为:[2kπ+$\frac{4π}{3}$,2kπ+$\frac{7π}{3}$],k∈Z;(kπ+$\frac{5π}{6}$,0),k∈Z;x=kπ+$\frac{π}{3}$,k∈Z.
点评 本题考查余弦函数的单调性和对称性,涉及整体的思想,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
已知点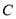
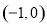 ,以
,以 为圆心的圆与直线
为圆心的圆与直线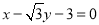 相切.
相切.
(1)求圆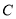 的方程;
的方程;
(2)如果圆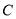 上存在两点关于直线
上存在两点关于直线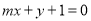 对称,求
对称,求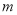 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
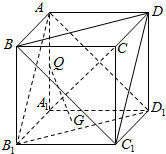 如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法:
如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com