
分析 (1)由条件利用正弦函数的单调性,求得函数的单调区间.
(2)由条件利用正弦函数的定义域和值域求得f(x)的取值范围.
解答 解:(1)对于函数f(x)=2sin(2x-$\frac{π}{4}$),令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,
求得kπ-$\frac{π}{8}$≤x≤kπ+$\frac{3π}{8}$,可得函数的增区间为[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$],k∈Z.
令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{3π}{8}$≤x≤kπ+$\frac{7π}{8}$,
可得函数的减区间为[kπ+$\frac{3π}{8}$,kπ+$\frac{7π}{8}$],k∈Z.
(2)若x∈[0,$\frac{3π}{4}$],则2x-$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{5π}{4}$],故f(x)∈[-$\sqrt{2}$,1].
点评 本题主要考查正弦函数的单调性,正弦函数的定义域和值域,属于基础题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
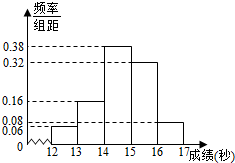 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
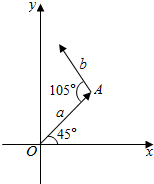 在直角坐标系中,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$如图所示,求它们的坐标.
在直角坐标系中,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$如图所示,求它们的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1≥-5 | B. | a1≥-1 | C. | a1≥-1或a1≤-5 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | (5,5) | C. | (5,6) | D. | (5,7) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com